Merge Sort is the matriarch of the sorting algorithm family. A source of wisdom for all her children (and a not-insignificant amount of "I told you so"), she is constantly looking out for her beloved sons and daughters.
The land on which the familial home sits has been in her family for generations, and will be for generations yet to come if she has anything to say about it.
She loves cooking and baking, and to be fair, makes a delicious turnover. But, and I can't stress this enough, don't try her lasagna. You will regret it.
That said, if she insists, make sure you have some Tums on hand and a bathroom nearby.

The Rundown
- Created By: John von Neumann (1945)
- Type: Divide-and-Conquer
- Stable? YES
- Best-Case: O(n log n)
- Average-Case: O(n log n)
- Worst-Case: O(n log n)
- Space Complexity: O(n)
- Sample Project: Over on GitHub
Algorithm
- BREAK the array into smaller subarrays.
- RECURSIVELY BREAK the smaller subarrays into yet smaller arrays.
- WHEN the arrays are at their smallest possible size (1), stop breaking them.
- RECURSIVELY MERGE the broken sub arrays back together in the correct order.
Visualization
A simple visualization would look like this:
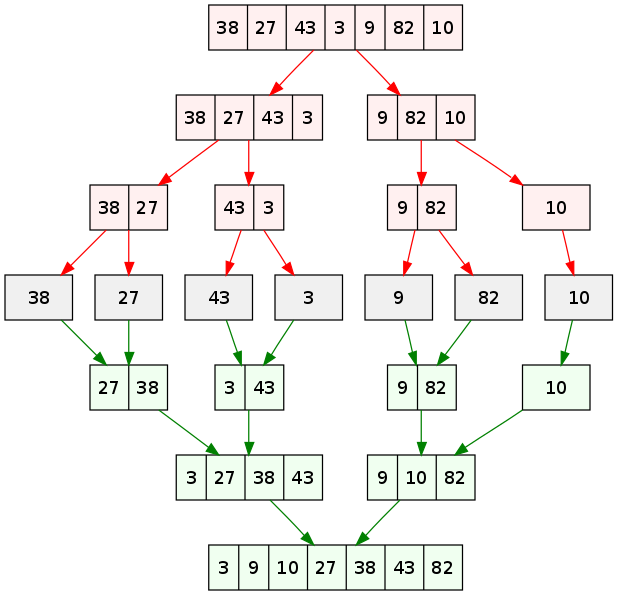
During each step of the process in red, the arrays are broken in half. Once each element of the original array is alone in its own array, the smaller arrays are merged back together in the correct order in the remaining steps.
This animated visualization from Wikipedia was also helpful:
Finally, don't forget to check out the "visualization and audibilization" of Merge Sort from YouTube:
C# Implementation
class MergeSort
{
static void Main(string[] args)
{
List<int> unsorted = new List<int>() { 42, 13, 86, 9, 10, 55, 71 };
List<int> sorted;
Random random = new Random(DateTime.Now.Millisecond);
Console.WriteLine("Merge Sort");
CommonFunctions.PrintInitial(unsorted);
sorted = Sort(unsorted);
CommonFunctions.PrintFinal(sorted);
Console.ReadLine();
}
//Uses recursion to break the collection
//into progressively smaller collections.
//Eventually, each collection will have just one element.
private static List<int> Sort(List<int> unsorted)
{
if (unsorted.Count <= 1)
{
return unsorted;
}
List<int> left = new List<int>();
List<int> right = new List<int>();
int median = unsorted.Count / 2;
for (int i = 0; i < median; i++) //Dividing the unsorted list
{
left.Add(unsorted[i]);
}
for (int i = median; i < unsorted.Count; i++)
{
right.Add(unsorted[i]);
}
left = Sort(left);
right = Sort(right);
return Merge(left, right);
}
//Method takes two sorted "sublists" (left and right)
//of original list and merges them into a new colletion
private static List<int> Merge(List<int> left, List<int> right)
{
List<int> result = new List<int>(); //The new collection
while (left.Any() || right.Any())
{
if (left.Any() && right.Any())
{
//Comparing the first element of each sublist
//to see which is smaller
if (left.First() <= right.First())
{
result.Add(left.First());
left.Remove(left.First());
}
else
{
result.Add(right.First());
right.Remove(right.First());
}
}
else if (left.Any())
{
result.Add(left.First());
left.Remove(left.First());
}
else if (right.Any())
{
result.Add(right.First());
right.Remove(right.First());
}
}
return result;
}
}Time and Space Complexity
In the best, average, and worst cases, Merge Sort has a time complexity of O(n log n). This is quite a bit better than Selection Sort, but our dear Merge Sort is savvy enough to not tell him that too often. After all, he knows it already.
What's not so great about Merge Sort is that it has a space complexity of O(n), meaning that it needs to use more memory than that taken up by the list to perform its algorithm. On small lists this is immaterial, but on large lists (e.g. those encountered in the real world) it could potentially cause things like Out of Memory errors.
Her book club, having sat through many long and winding tales always ending with "if only they'd listened to me," feels the same way.
Summary
Merge Sort, the devoted mother and grandmother of the family, is quite an algorithm. Wise, caring, and a terrible cook, she is a formidable woman with a lot to give and will gladly make you something to eat even if you just ate. You will still want those Tums, though.
Next up in the reunion is the eldest child, Insertion Sort. Watch your money around her!

Don't forget to check out the sample project over on GitHub!
Happy Coding!








