Comb Sort is the poster boy for the all-American child.

Unlike his elder brother Shell Sort, Comb Sort is a star athlete. He started as the quarterback for his high school football team when he was a sophomore. But more than that, he has everything he thought he could ever want, at least until recently. He's the junior prom king, the one voted "best athlete" in the yearbook, everything. Life has been easy for him so far.

Yet, something is bothering him. Something that, until recently, he couldn't describe.

O-ma-HA! Photo by Riley McCullough / Unsplash

He's not the smartest guy, and he knows this. His grades are mostly Cs and Ds, and he understands that that doesn't bode well for his future. His parents are high-achievers, his brother is a straight-A student, and he's... what? A star athlete? That won't last forever. What happens when he can no longer get by on physical prowess?

So, he reads. He studies. He's putting more time into making good test scores and less time into sports. It's not working yet (his last test was a C+), but he's hopeful that it will, and soon. He can't get through life on athletic skills alone. He's sorting out his life, one piece at a time.

The Rundown

exceptionnotfound/SortExtravaganzaCSharp
Lots of example sorting algorithms, from a family reunion. - exceptionnotfound/SortExtravaganzaCSharp
GitHubexceptionnotfound
Project for this post: CombSort

Algorithm

  1. DETERMINE the appropriate gap size h by using a set shrink factor k.
  2. COMPARE each pair of elements that are h distance from each other.
  3. SWAP those elements if they are in the wrong order.
  4. COMPLETE a pass through the array with the selected h.
  5. SHRINK the gap size h using shrink factor k.
  6. IF h is not 1, GOTO step 2.
  7. CONTINUE until h is 1 AND a pass through the array results in no swaps.

Visualization

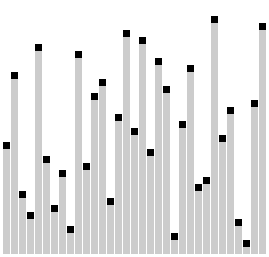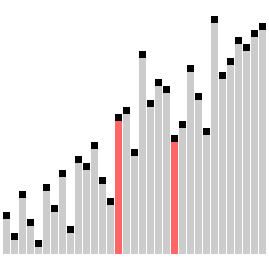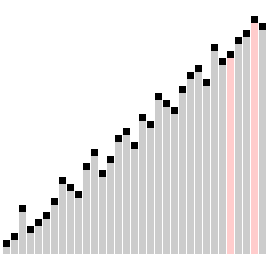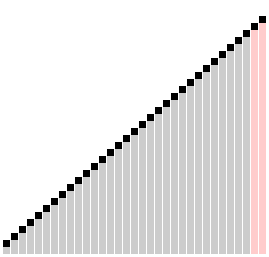
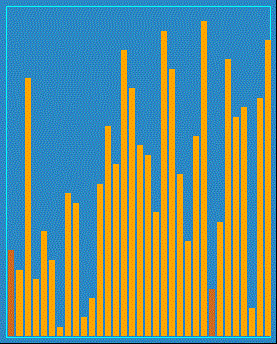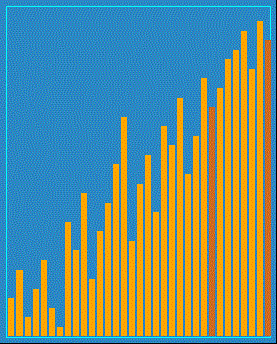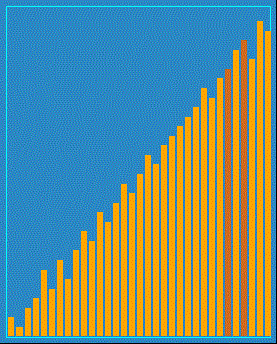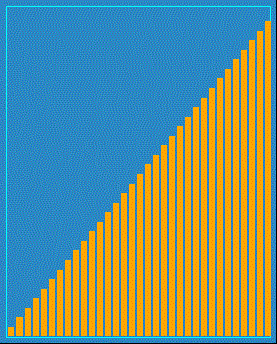
You can see from this animation why this algorithm got the name "Comb Sort": the comparison distance look like two prongs in a comb. You can also see that this is a not-very-effective sort: it has to do many passes through all elements in order to fully sort this list. In fact, we would most likely consider Comb Sort to be a "naive" sort, on the same level as Selection Sort.

Also check out the "audibilization" of this sort from YouTube:

Finally, reader James Curran kindly created a visualization for this sort; it looks like this:

C# Implementation

class CombSort
{
    static int GetNextGap(int gap)
    {
        //The "shrink factor", empirically shown to be 1.3
        gap = (gap * 10) / 13;
        if (gap < 1)
        {
            return 1;
        }
        return gap;
    }

    static void Sort(int[] array)
    {
        int length = array.Length;

        int gap = length;

        //We initialize this as true to enter the while loop.
        bool swapped = true;

        while (gap != 1 || swapped == true)
        {
            gap = GetNextGap(gap);

            //Set swapped as false.  Will go to true when two values are swapped.
            swapped = false;

            //Compare all elements with current gap 
            for (int i = 0; i < length - gap; i++)
            {
                if (array[i] > array[i + gap])
                {
                    //Swap
                    int temp = array[i];
                    array[i] = array[i + gap];
                    array[i + gap] = temp;

                    swapped = true;
                }
            }
        }
    }

    public static void Main()
    {
        int[] array = { 10, 28, 1, 55, 6, 21, 36, 3, 45, 15, 0 };

        Console.WriteLine("Comb Sort");

        CommonFunctions.PrintInitial(array);

        Sort(array);

        CommonFunctions.PrintFinal(array);
        Console.ReadLine();

    }
}

Time and Space Complexity

The worst case of O(n2) make intuitive sense, at least to me. Given that comb sort is based on bubble sort, we would expect poor time complexities for it. But the average case is interesting because it introduces a form of notation I hadn't seen before: big-omega.

Remember that the average time complexity for this algorithm is Ω(n2/2p). This is read aloud as "big-omega of n-squared over 2 to the power of p". But what does big-omega mean? In short, big-omega represents the best possible case of the complexity. On average, comb sort has been shown to perform no better than n2/2p, where n is the length of the unsorted array and p is the number of times we have to decrement the gap.

This is not a great time, and because it's the best possible case on average, we can conclude that Comb Sort is not an efficient sorting algorithm.

Summary

Comb Sort is a relatively-inefficient algorithm that aims to sort a collection by comparing two elements across h distance, swapping them if they are out of order, and then slowly shrinking that distance. He's hoping he can get his academic life in order before his athletic skills run out. Slowly, surely, he's making that dream come true, one test at a time.

The family's consummate overachiever, Quick Sort, is next up.

QuickSort in C#
QuickSort is a recursive sorting algorithm that wishes he could slow down a bit.
Exception Not FoundMatthew Jones

Don't forget to check out the sample project over on GitHub!

Happy Coding!