I'm an adult, most of the time. That means I have to do adult things, like getting groceries or gas or maintaining our yard. I am also married with three kids. And that means a LOT of laundry.
Laundry by itself isn't too bad. It gives my easily-distracted brain a simple, repetitive task that often allows me to think more clearly than is otherwise possible. But the worst part of laundry, the absolute worst, is the socks.

Matching socks from five individuals, each with different styles, colors, lengths, etc. is a huge, time-consuming task. Frequently my beloved wife and I dedicate a whole day to just doing laundry (and other house-related chores) and we have to save the socks until the very end, because otherwise we end up with massive piles of unmatched foot wrappers. But even that takes enormous amounts of time and effort; we pick a sock, and scan the pile for it's mate. This is terribly inefficient.
Whatever else I am, I'm also a programmer. And I am not content to let a good problem, that of how to efficiently sort socks, go to waste.
In this post, we're going to see five SIX different potential solutions to sorting a huge pile of socks. These five solutions exist in the corresponding sample C# project on GitHub. We'll walk through why some are better than others, and hopefully come up with a way to efficiently sort socks.
Program Setup
Here's some of the code I wrote to set up this problem. We need a class Sock, a SockGenerator, some enumerations, and a method which checks to see if the socks are well and truly sorted.
public class Sock
{
public SockColor Color { get; set; }
public SockOwner Owner { get; set; }
public SockLength Length { get; set; }
}
public enum SockColor
{
Red,
Blue,
Green,
Black,
White
}
public enum SockLength
{
NoShow, //Disappears beneath the shoe line
Ankle, //Shows over shoe line, covers ankle
Crew //Comes partway up the calf, but no higher than halfway
}
public enum SockOwner
{
AdultMan,
AdultWoman,
Child
}
public static class SockGenerator
{
public static List<Sock> GenerateSocks(int max)
{
int count = 0;
List<Sock> socks = new List<Sock>(max);
//Generate a certain number of pairs of socks
//If the "max" is an odd number, we still generate pairs,
//(e.g. all socks will have a match).
while(count < max)
{
var pair = GeneratePair();
socks.Add(pair[0]);
socks.Add(pair[1]);
count = count + 2;
}
return socks.OrderBy(x => Guid.NewGuid()).ToList();
}
private static List<Sock> GeneratePair()
{
List<Sock> pair = new List<Sock>();
Random random = new Random();
var sockOwner = random.Next(0, 3);
var sockColor = random.Next(0, 5);
var sockLength = random.Next(0, 3);
var sock = new Sock()
{
Owner = (SockOwner)sockOwner,
Color = (SockColor)sockColor,
Length = (SockLength)sockLength
};
pair.Add(sock);
pair.Add(sock);
return pair;
}
//This method checks to see if all socks
//are in order with their matching pair.
public static bool AreMatched(List<Sock> socks)
{
bool areMatched = true;
for(int i = 0; i < socks.Count; i = i + 2)
{
var firstSock = socks[i];
var secondSock = socks[i + 1];
areMatched = areMatched
&& firstSock.Color == secondSock.Color
&& firstSock.Owner == secondSock.Owner
&& firstSock.Length == secondSock.Length;
if (areMatched == false) break;
}
return areMatched;
}
}
We can now generate a collection of socks, and confirm if that collection is sorted.
Goals
The primary goal of this exercise is to find a sorting and pairing solution that performs reasonably well for an arbitrarily large number of socks. Ideally we will also find something that works in the real world, but given that we programmers so rarely inhabit such a place, this would be a nice bonus rather than a must-have.
To check this goal, we will measure the time each solution takes to sort 500k (five hundred thousand) socks using the very nice Stopwatch class in .NET.
Solution #1: Naive Sort
Let's start our solutions with the simplest one: a naive sort.
The idea goes like this: pick any sock, then iterate over the entire collection of socks until you find a match. Place the paired socks in a different pile.
Algorithm
- GIVEN a collection of unmatched socks.
- TAKE the first sock.
- LOOK at each sock in order until you find one that matches on all properties.
- MOVE the matching pair to a new collection.
Implementation
public class Sorter
{
//1. GIVEN a collection of unmatched socks
public List<Sock> NaiveSort(List<Sock> unmatchedSocks)
{
Stopwatch watch = new Stopwatch();
watch.Start();
List<Sock> matchedSocks = new List<Sock>();
while(unmatchedSocks.Any())
{
//2. TAKE the first sock
Sock currentSock = unmatchedSocks[0];
unmatchedSocks.Remove(currentSock);
Sock matchingSock;
//3. LOOK at each sock in order until you find a match on all properties
foreach(var tempSock in unmatchedSocks)
{
if(tempSock.Color == currentSock.Color
&& tempSock.Length == currentSock.Length
&& tempSock.Owner == currentSock.Owner)
{
//4. MOVE the matching socks to a new collection
matchingSock = tempSock;
unmatchedSocks.Remove(tempSock);
matchedSocks.Add(currentSock);
matchedSocks.Add(tempSock);
break;
}
}
}
watch.Stop();
Console.WriteLine("Completed Naive Sort in " + watch.ElapsedMilliseconds.ToString() + " milliseconds.");
return matchedSocks;
}
}
Testing
Let's run our app, with 500k socks, and see if we get a reasonable time to sort.
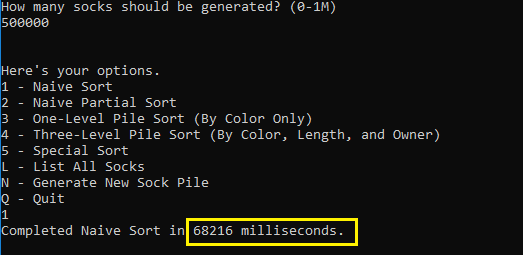
It took approximately 68 seconds to sort 500k socks. This is now our baseline. Our subsequent solutions should all perform better than this.
Solution #2: Naive Partial Sort
So the naive sort isn't great, but it gets the job done. Now we just want to improve on it.
One simple way of improving on it would be to say that we only care about matching by one property; e.g. we only want to match on owner and not care about the length or color. In theory, this allows us to stop searching the pile for a "match" earlier than in the basic Naive Sort. Hence, our Naive Partial Sort solution.
Algorithm
- GIVEN a collection of unmatched socks.
- TAKE the first sock.
- LOOK at each sock in order until you find one that matches on ONLY ONE property.
- MOVE the "matching" pair to a new collection.
Implementation
public List<Sock> NaivePartialSort(List<Sock> unmatchedSocks)
{
Stopwatch watch = new Stopwatch();
watch.Start();
List<Sock> matchedSocks = new List<Sock>();
while (unmatchedSocks.Any())
{
//Get the sock at the top of the pile
Sock currentSock = unmatchedSocks[0];
unmatchedSocks.Remove(currentSock);
Sock matchingSock;
//Iterate through the unmatched socks to find the next one that matches, ignoring color and length.
foreach (var tempSock in unmatchedSocks)
{
if (tempSock.Owner == currentSock.Owner)
{
matchingSock = tempSock;
unmatchedSocks.Remove(tempSock);
matchedSocks.Add(currentSock);
matchedSocks.Add(tempSock);
break;
}
}
}
watch.Stop();
Console.WriteLine("Completed Naive Partial Sort in " + watch.ElapsedMilliseconds.ToString() + " milliseconds.");
return matchedSocks;
}
Testing
With a new set of 500k socks, here's how our Naive Partial Sort performs:
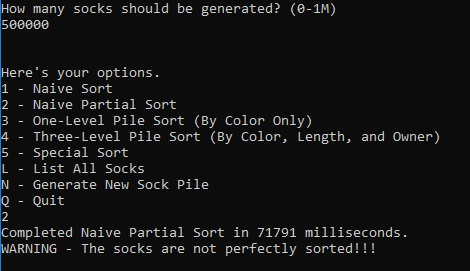
This test took 71.8 seconds to run, which is longer than the basic Naive Sort.
I've run this test several times, and each time the Naive Partial Sort take a few seconds longer than the basic Naive Sort. It's very possible this is simply due to small sample size errors, but if any of my dear readers sees a reason why the Naive Partial Sort would consistently perform worse than the Naive Sort, I'd be happy to hear it. UPDATE: Comments below explain why the Naive Partial Sort performs worse than the base Naive Sort.
Anyway, clearly we aren't going to get any better performance out of a naive-type sorting algorithm. We need to think about the problem differently.
Solution #3: One-Level Pile Sort
With the naive, pick-a-sock-then-find-its-mate solutions not working terribly well, it's time we find a new solution. Maybe we could introduce another layer of abstraction and "pre-sort" the socks before matching them?

Here's the idea: if we sort the socks from the big combined pile into smaller, attribute-based piles (e.g. by color, by length, or by owner) then we could use the Naive Sort to sort the smaller piles, and it should take a lot less time.
Algorithm
- GIVEN a pile of unmatched socks
- SORT each sock into another pile based on a single attribute (color OR length, etc.)
- FOR EACH of these piles...
- TAKE the first sock in the pile.
- LOOK at each sock in the sub pile in order until you find a match.
- MOVE the matching pair to a new collection.
You will notice that steps 4, 5, and 6 are just the steps from the Naive Sort again.
Implementation
//1. GIVEN a pile of unmatched socks.
public List<Sock> OneLevelPileSort(List<Sock> socks)
{
Stopwatch watch = new Stopwatch();
watch.Start();
//2. SORT each sock into another pile based on a single attribute.
var colorSortedSocks = SplitByColor(socks); //Implementation below
//3. FOR EACH of these piles...
//4. TAKE the first sock in the pile.
//5. LOOK at each sock in the sub pile in order until you find a match.
//6. MOVE the matching pair to a new collection.
List<Sock> matchedSocks = new List<Sock>();
matchedSocks.AddRange(NaiveSort(colorSortedSocks[0]));
matchedSocks.AddRange(NaiveSort(colorSortedSocks[1]));
matchedSocks.AddRange(NaiveSort(colorSortedSocks[2]));
matchedSocks.AddRange(NaiveSort(colorSortedSocks[3]));
matchedSocks.AddRange(NaiveSort(colorSortedSocks[4]));
watch.Stop();
Console.WriteLine("Completed One-Level Pile Sort in " + watch.ElapsedMilliseconds.ToString() + " milliseconds.");
return matchedSocks;
}
public List<List<Sock>> SplitByColor(List<Sock> socks)
{
List<List<Sock>> colorSortedSocks = new List<List<Sock>>();
//Initialize the lists
colorSortedSocks.Add(new List<Sock>());//0 Red
colorSortedSocks.Add(new List<Sock>());//1 Blue
colorSortedSocks.Add(new List<Sock>());//2 Green
colorSortedSocks.Add(new List<Sock>());//3 Black
colorSortedSocks.Add(new List<Sock>());//4 White
foreach (var sock in socks)
{
switch (sock.Color)
{
case SockColor.Red:
colorSortedSocks[0].Add(sock);
break;
case SockColor.Blue:
colorSortedSocks[1].Add(sock);
break;
case SockColor.Green:
colorSortedSocks[2].Add(sock);
break;
case SockColor.Black:
colorSortedSocks[3].Add(sock);
break;
case SockColor.White:
colorSortedSocks[4].Add(sock);
break;
}
}
return colorSortedSocks;
}
Testing
Here's the output we get for running this sort against 500k socks:
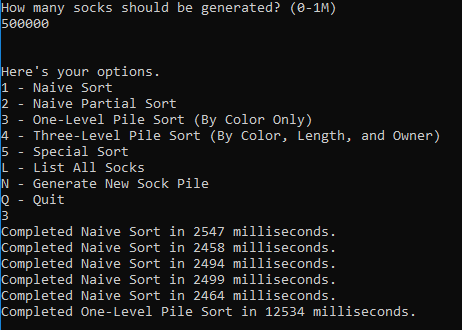
The one-level pile sort sorted 500k socks in 12.5 seconds, more than five times as quickly as the naive sort implementation! We're on to something now!
We need to try something... bigger.
Solution #4: N-Level Pile Sort
This is the logical conclusion to the one-level pile sort: if sorting into piles based on one attribute was quicker than the naive solution, then most likely sorting into progressively smaller piles will be quicker still.
The idea here is to get the socks sorted into small-enough piles so that these piles do not themselves need to be sorted further.
Algorithm
- GIVEN a pile of unmatched socks.
- SORT each sock into a pile based on one attribute.
- FOR EACH attribute, sort the new piles into smaller piles, where all of the socks in that pile match on all sorted attributes.
- MOVE each pair from the smallest-possible piles into a new collection (there will be no sorting here).
Implementation
Note that our implementation is not generic for N properties; it is specific to our known properties of Owner, Length, and Color.
public List<Sock> ThreeLevelPileSort(List<Sock> socks)
{
Stopwatch watch = new Stopwatch();
watch.Start();
var colorSortedSocks = SplitByColor(socks);
List<Sock> matchedSocks = new List<Sock>();
foreach (var colorSortedPile in colorSortedSocks)
{
var lengthSortedPiles = SplitByLength(colorSortedPile);
foreach(var lengthSortedPile in lengthSortedPiles)
{
var ownerSortedPiles = SplitByOwner(lengthSortedPile);
foreach(var ownerSortedPile in ownerSortedPiles)
{
foreach(var sock in ownerSortedPile)
{
matchedSocks.Add(sock);
}
}
}
}
watch.Stop();
Console.WriteLine("Completed Three-Level Pile Sort in " + watch.ElapsedMilliseconds.ToString() + " milliseconds.");
return matchedSocks;
}
public List<List<Sock>> SplitByColor(List<Sock> socks)
{
List<List<Sock>> colorSortedSocks = new List<List<Sock>>();
//Initialize the lists
colorSortedSocks.Add(new List<Sock>());//0 Red
colorSortedSocks.Add(new List<Sock>());//1 Blue
colorSortedSocks.Add(new List<Sock>());//2 Green
colorSortedSocks.Add(new List<Sock>());//3 Black
colorSortedSocks.Add(new List<Sock>());//4 White
foreach (var sock in socks)
{
switch (sock.Color)
{
case SockColor.Red:
colorSortedSocks[0].Add(sock);
break;
case SockColor.Blue:
colorSortedSocks[1].Add(sock);
break;
case SockColor.Green:
colorSortedSocks[2].Add(sock);
break;
case SockColor.Black:
colorSortedSocks[3].Add(sock);
break;
case SockColor.White:
colorSortedSocks[4].Add(sock);
break;
}
}
return colorSortedSocks;
}
public List<List<Sock>> SplitByLength(List<Sock> socks)
{
List<List<Sock>> colorSortedSocks = new List<List<Sock>>();
//Initialize the lists
colorSortedSocks.Add(new List<Sock>());//0 NoShow
colorSortedSocks.Add(new List<Sock>());//1 Ankle
colorSortedSocks.Add(new List<Sock>());//2 Crew
foreach (var sock in socks)
{
switch (sock.Length)
{
case SockLength.NoShow:
colorSortedSocks[0].Add(sock);
break;
case SockLength.Ankle:
colorSortedSocks[1].Add(sock);
break;
case SockLength.Crew:
colorSortedSocks[2].Add(sock);
break;
}
}
return colorSortedSocks;
}
public List<List<Sock>> SplitByOwner(List<Sock> socks)
{
List<List<Sock>> colorSortedSocks = new List<List<Sock>>();
//Initialize the lists
colorSortedSocks.Add(new List<Sock>());//0 AdultMan
colorSortedSocks.Add(new List<Sock>());//1 AdultWoman
colorSortedSocks.Add(new List<Sock>());//2 Child
foreach (var sock in socks)
{
switch (sock.Owner)
{
case SockOwner.AdultMan:
colorSortedSocks[0].Add(sock);
break;
case SockOwner.AdultWoman:
colorSortedSocks[1].Add(sock);
break;
case SockOwner.Child:
colorSortedSocks[2].Add(sock);
break;
}
}
return colorSortedSocks;
}
Testing
Here's the time it takes to sort 500k unmatched socks with the n-level pile sort:
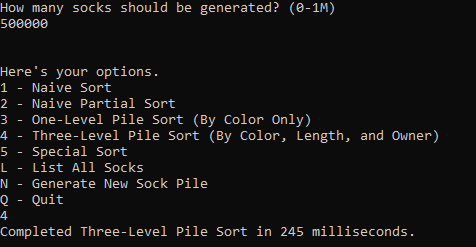
The n-level pile sort took less than a second (245 milliseconds) to sort all the socks. That's a hell of an improvement over the Naive Sorts.
What Does All This Mean?
It means I've been doing laundry wrong my entire life.
More practically speaking, it means that we need to think more clearly about how to iterate over a collection when attempting to sort said collection. The problem with the naive sorts isn't that they work, it's that they're not efficient. By subdividing the main pile of socks into progressively smaller and smaller piles, we dramatically increase our efficiency.
Conclusion
Sorting socks in the real world is a time-consuming process; but we can use computer science ideas to make it quite a bit more efficient. The n-level pile sort (throwing the socks into progressively smaller piles where they match on all attributes) is clearly the most efficient way to sort socks that we've discussed.
Or, at least, the second most efficient.
public List<Sock> SpecialSort(List<Sock> socks)
{
Stopwatch watch = new Stopwatch();
watch.Start();
watch.Stop();
Console.WriteLine("Completed Special Sort in " + watch.ElapsedMilliseconds.ToString() + " milliseconds.");
Console.WriteLine("Nobody cares about matching socks anyway.");
return socks;
}
Don't forget to check out the sample project over on GitHub!
Happy Coding!
Bonus Solution #6: Dictionary Sort
But wait, there's more! Courtesy of Thomas Levesque, here's another sorting solution, which he termed Dictionary Sort.
Implementation
public List<Sock> DictionarySort(List<Sock> unmatchedSocks)
{
Stopwatch watch = new Stopwatch();
watch.Start();
List<Sock> matchedSocks = new List<Sock>();
var waitingForMatch = new Dictionary<(SockOwner, SockColor, SockLength), Sock>();
while (unmatchedSocks.Any())
{
int index = unmatchedSocks.Count - 1;
var sock = unmatchedSocks[index];
unmatchedSocks.RemoveAt(index);
var key = (sock.Owner, sock.Color, sock.Length);
if (waitingForMatch.TryGetValue(key, out var matchingSock))
{
matchedSocks.Add(sock);
matchedSocks.Add(matchingSock);
waitingForMatch.Remove(key);
}
else
{
waitingForMatch.Add(key, sock);
}
}
watch.Stop();
Console.WriteLine("Completed Dictionary Sort in " + watch.ElapsedMilliseconds.ToString() + " milliseconds.");
return matchedSocks;
}
Testing
The sample run of 500k socks produced this result:
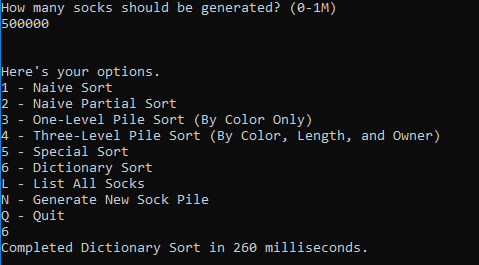
As you can see, this is comparable to the Three-Level Pile Sort from earlier, in that it is blazing fast and accurate. Make sure to thank Thomas for contributing this result!