Modeling Practice: UNO in C# Part 2 - Player Behavior

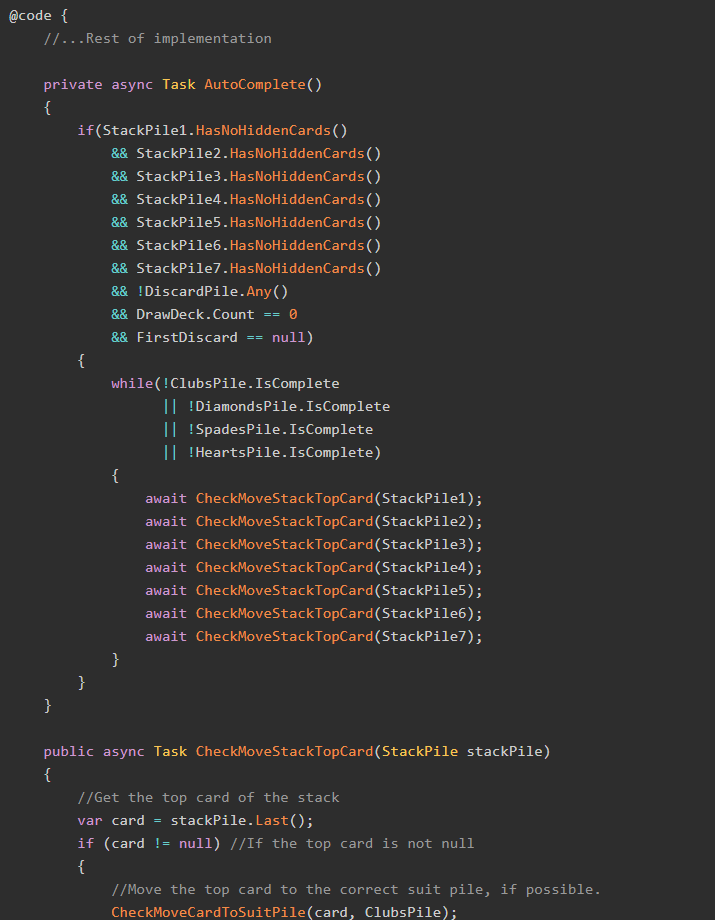
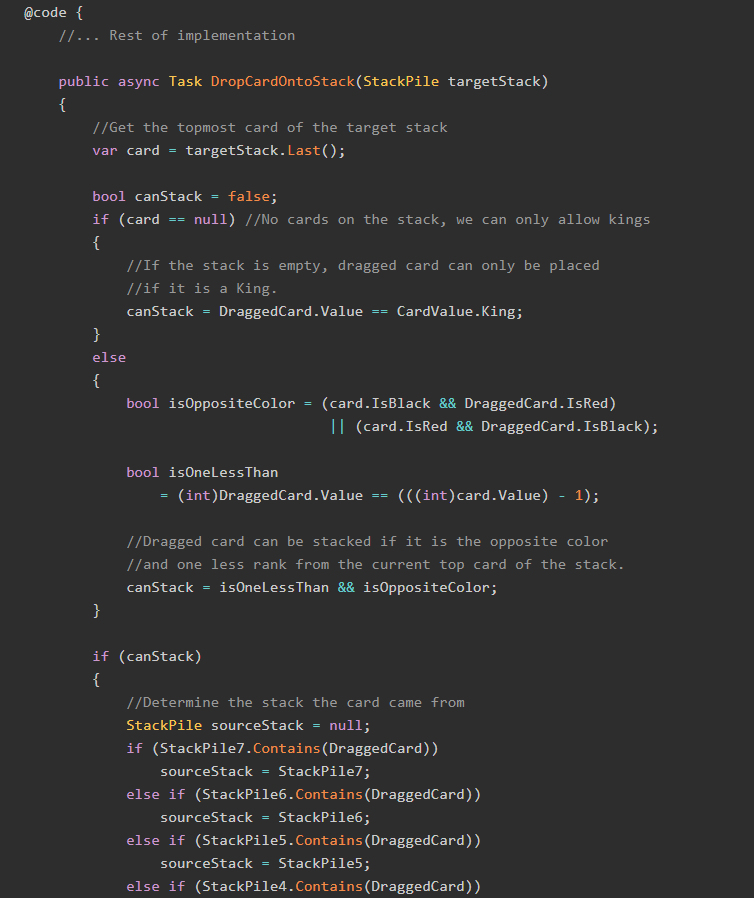
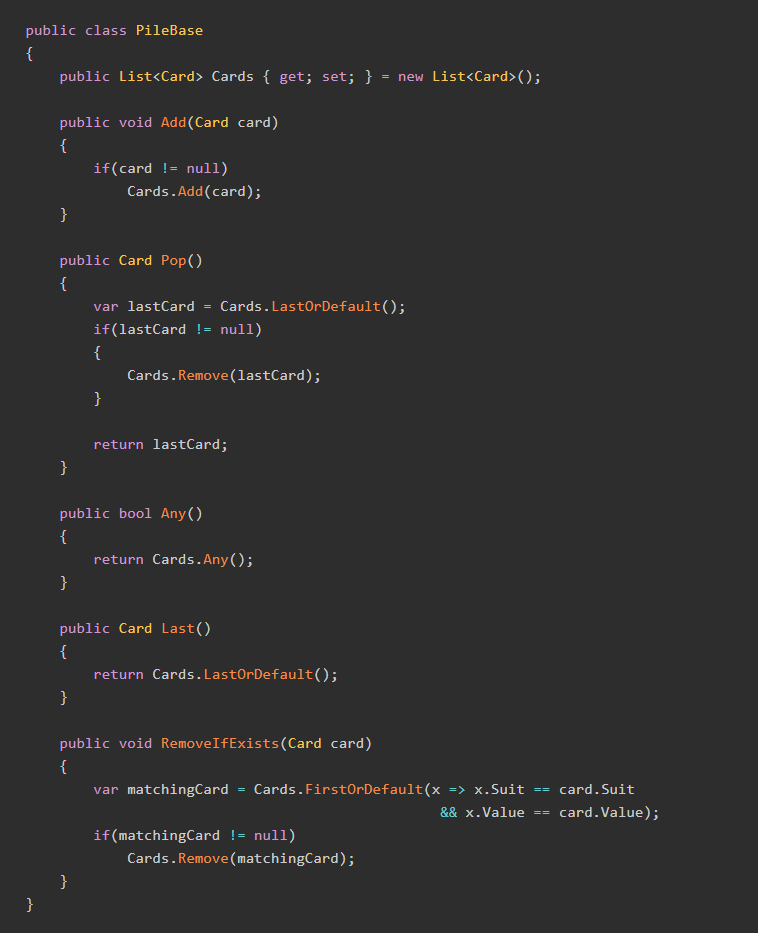
Note: This post is the second in a three-part series which attempts to model the card game UNO as a C# application. Here's Part One. You may want to use the GitHub repository to follow along.

Now that we have modeled the cards and the draw pile, we come to the first really tricky part of this modeling practice: we must model the players of the game AND how they will behave during the game itself.

The first part (modeling the players themselves) is simpler, and so we will do it first. A "player" in this game is really just a set of cards (the "hand"), the position that the player is sitting in (first, second, third, etc.) and the logic the player uses to decide which card to play. The simplest possible player class would then look like this:

public class Player
{
    public List<Card> Hand { get; set; }

    //This determines the starting turn order
    public int Position { get; set; } 

    public Player()
    {
        Hand = new List<Card>();
    }
}

The problem with this simple class is that it leaves out the logic the player must use to determine which card s/he wants to play. That logic is not simple, and in my model it takes quite a few steps to work out.

Assumptions

First, we need to make some critical assumptions. There is no mathematical way to have a "perfect" game of UNO, so our players will often need to decide which card to play of two or they could play.

First, we must remember a few rules from earlier:

• A player playing a card must match the current discard by either color or value, or play a regular Wild card.
• A player following a Wild card must match the color declared by the person who laid that card down.
• A player cannot use a Wild Draw Four card if another card in his/her hand can be played.

Those rules leave a lot of possible situations up to interpretation. For example, if the current discard is a Green Five and I have a Green Skip and a Yellow 5, which should I play?

I've made this model a bit simpler by assuming that my players are stupid jackasses.

That is, every time a player has to make a decision about which card to play, s/he will always play the card that causes the most pain to the next player, regardless of his/her own strategic situation. If I can play a Skip or a 7, I'm playing the Skip (and Lord help you if I have a Draw Two).

Also, if a player has no matches, they must draw a card. If that card can play, then the player will play it; otherwise, his/her turn is over and play moved to the next player.

The PlayerTurn Object

UNO is also a bit different than other games we've modeled (Candy Land, Minesweeper) because the actions of a player have a direct consequence on the next player. We will need our players to take that into account, and they must abide by whatever the "attacking" card says they do.

Therefore, in order for the player to know what action s/he must take, we need the player to be aware of what happened on the previous player's turn. To model the actions taken by a player, we will use the PlayerTurn object, which looks like this:

public class PlayerTurn
{
    public Card Card { get; set; }
    public CardColor DeclaredColor { get; set; } //Used mainly for Wild cards
    public TurnResult Result { get; set; }
}

The TurnResult enum has all the possible situations which arise from a player completing his/her turn. Those values are as follows:

public enum TurnResult
{
    //Start of game.
    GameStart,

    //Player played a normal number card.
    PlayedCard,
        
    //Player played a skip card.
    Skip,

    //Player played a draw two card.
    DrawTwo,

    //Player was forced to draw by other player's card.
    Attacked,

    //Player was forced to draw because s/he couldn't match the current discard.
    ForceDraw,

    //Player was forced to draw because s/he couldn't match the current discard, but the drawn card was playable.
    ForceDrawPlay,

    //Player played a regular wild card.
    WildCard,

    //Player played a draw-four wild card.
    WildDrawFour,

    //Player played a reverse card.
    Reversed
}

Each player takes a turn, and the action performed during that turn are represented by the PlayerTurn object. When the next player takes his/her turn, s/he will also receive the PlayerTurn object for the previous player's turn.

Player Order of Operations

With all the assumptions and the PlayerTurn object in place, let's lay out a skeleton for how our stupid jackass players will behave. Here's how each player will act during his/her turn.

1. If the previous player "attacked" the current player (via a Skip, a Draw Two, or a Draw Four), then the current player must suffer the attack.
2. If the current player can play an "attacking" card (within the rules), then s/he does so.
3. If the current player can play a number card, then s/he does so.
4. If the current player has no matching cards except a Wild card, s/he plays the Wild. The current player will then declare the color to be the one s/he has the most cards of (the declared color is random if the current player has the same number of card in two or more colors).
5. If the current player has no cards to play, s/he draws a single card from the draw pile. If the drawn card can be played, s/he plays that card.

NOTE: In either step 2 or step 3, if the player has many possible cards to play, s/he will play the one which results in the color s/he has the most of.

All of those steps are pretty straightforward, but let me explain the reasoning behind Step 4. If we have only one card left, and that card is a Wild card, we are guaranteed to discard our final card on our next turn. Therefore, it behooves the players to hold on to Wild cards until the last possible moment.

Now comes the tricky part; how in the world do we model this?

Being Attacked

Let's start with Step 1 in our Player Order of Operations:

Step 1: If the previous player "attacked" the current player (via a Skip, a Draw Two, or a Draw Four), then the current player must suffer the attack.

The interesting thing about being "attacked" is that being attacked always results in the current player not being able to discard a card. This is why a Reverse card is not an attacking card.

So, let's create a method called ProcessAttack(), during which we will create a PlayerTurn object representing what action the current player took during his/her turn (when s/he suffered the attack).

private PlayerTurn ProcessAttack(Card currentDiscard, CardDeck drawPile)
{
    PlayerTurn turn = new PlayerTurn();
    turn.Result = TurnResult.Attacked;

    //The player after the current player must match the card that attacked the current player; hence we pass those values through to the next PlayerTurn.
    turn.Card = currentDiscard; 
    turn.DeclaredColor = currentDiscard.Color;

    if(currentDiscard.Value == CardValue.Skip)
    {
        Console.WriteLine("Player " + Position.ToString() + " was skipped!");
    }
    else if(currentDiscard.Value == CardValue.DrawTwo)
    {
        Console.WriteLine("Player " + Position.ToString() + " must draw two cards!");
        Hand.AddRange(drawPile.Draw(2));
    }
    else if(currentDiscard.Value == CardValue.DrawFour)
    {
        Console.WriteLine("Player " + Position.ToString() + " must draw four cards!");
        Hand.AddRange(drawPile.Draw(4));
    }

    return turn;
}

On the Offensive

If the current player is not attacked, s/he will attempt to play an attacking card that matches the color or value of the current discard. Let's create several methods which will make the player decide which card to play.

public PlayerTurn PlayTurn(PlayerTurn previousTurn, CardDeck drawPile) { }

private PlayerTurn DrawCard(PlayerTurn previousTurn, CardDeck drawPile) { }

private bool HasMatch(Card card) { }

private bool HasMatch(CardColor color) { }

private PlayerTurn PlayMatchingCard(CardColor color) { }

private PlayerTurn PlayMatchingCard(Card currentDiscard) { }

private CardColor SelectDominantColor() { }

Notice the overloads for HasMatch() and PlayMatchingCard(). One of the quirks of this model is that, whenever a player plays a Wild card, s/he declares a color to be played; the next discard can only be matched on color, not value. For my model, I decided to make matching color or value vs matching color only two completely separate "thought processes" as it were.

We'll start with a skeleton of the PlayTurn() method, since it will need to call the ProcessAttack() method we defined earlier. Here's an outline of this method:

public PlayerTurn PlayTurn(PlayerTurn previousTurn, CardDeck drawPile)
{
    PlayerTurn turn = new PlayerTurn();

    //If the current player was attacked
    if (previousTurn.Result == TurnResult.Skip
        || previousTurn.Result == TurnResult.DrawTwo
        || previousTurn.Result == TurnResult.WildDrawFour)
    {
        return ProcessAttack(previousTurn.Card, drawPile);
    }

    //When the current discard is a Wild card
    else if ((previousTurn.Result == TurnResult.WildCard 
                || previousTurn.Result == TurnResult.Attacked 
                || previousTurn.Result == TurnResult.ForceDraw) 
                && previousTurn.Card.Color == CardColor.Wild
                && HasMatch(previousTurn.DeclaredColor))
    {
        turn = PlayMatchingCard(previousTurn.DeclaredColor);
    }
    
    //When the current discard is a non-wild card
    else if (HasMatch(previousTurn.Card))
    {
        turn = PlayMatchingCard(previousTurn.Card);
    }

    //When the player has no matching cards
    else //Draw a card and see if it can play
    {
        turn = DrawCard(previousTurn, drawPile);
    }

    DisplayTurn(turn);
    return turn;
}

Let's remind ourselves of Player Logic Steps 2, 3, and 4, as well as the pertinent note:

Step 2: If the player can play an "attacking" card (within the rules), then s/he does so.

Step 3: If the player can play a number card, then s/he does so.

Step 4: If the player has no matching cards except a Wild card, s/he plays the Wild. The player will then declare the color to be the one s/he has the most cards of (the color is random if the player has the same number of card in two or more colors).

NOTE: In either step 2 or step 3, if the player has many possible cards to play, s/he will play the one which results in the color s/he has the most of.

With these steps in mind, let's start building the PlayMatchingCard() methods.

Matching a Wild

If the card we need to match is a Wild, we will need to use the property DeclaredColor in the PlayerTurn object. We must play a card of that color.

Here's the code for the Wild card version of PlayMatchingCard() (the logic involved in the method is in the comments):

private PlayerTurn PlayMatchingCard(CardColor color)
{
    var turn = new PlayerTurn();
    turn.Result = TurnResult.PlayedCard;
    var matching = Hand.Where(x => x.Color == color || x.Color == CardColor.Wild).ToList();

    //We cannot play wild draw four unless there are no other matches.  But if we can play it, we must.
    if (matching.All(x => x.Value == CardValue.DrawFour))
    {
        turn.Card = matching.First();
        turn.DeclaredColor = SelectDominantColor();
        turn.Result = TurnResult.WildCard;
        Hand.Remove(matching.First());

        return turn;
    }

    //Otherwise, we play the card that would cause the most damage to the next player.
    if (matching.Any(x => x.Value == CardValue.DrawTwo))
    {
        turn.Card = matching.First(x => x.Value == CardValue.DrawTwo);
        turn.Result = TurnResult.DrawTwo;
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(turn.Card);

        return turn;
    }

    if (matching.Any(x => x.Value == CardValue.Skip))
    {
        turn.Card = matching.First(x => x.Value == CardValue.Skip);
        turn.Result = TurnResult.Skip;
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(turn.Card);

        return turn;
    }

    if (matching.Any(x => x.Value == CardValue.Reverse))
    {
        turn.Card = matching.First(x => x.Value == CardValue.Reverse);
        turn.Result = TurnResult.Reversed;
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(turn.Card);

        return turn;
    }

    //If we cannot play an "attacking" card, we play any number card
    var matchOnColor = matching.Where(x => x.Color == color);
    if (matchOnColor.Any())
    {
        turn.Card = matchOnColor.First();
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(matchOnColor.First());

        return turn;
    }

    //We only play a regular Wild card if we have no other matches
    if (matching.Any(x => x.Value == CardValue.Wild))
    {
        turn.Card = matching.First(x => x.Value == CardValue.Wild);
        turn.DeclaredColor = SelectDominantColor();
        turn.Result = TurnResult.WildCard;
        Hand.Remove(turn.Card);

        return turn;
    }

    //This should never happen
    turn.Result = TurnResult.ForceDraw;
    return turn;
}

Matching a Non-Wild

Now we must consider the situation when the current discard is not a wild card. In my model, the code for this method is very, very similar to the Wild situation, but I couldn't figure out an appropriate way to separate them sanely. Anyway, here's the non-wild version of PlayMatchingCard():

private PlayerTurn PlayMatchingCard(Card currentDiscard)
{
    var turn = new PlayerTurn();
    turn.Result = TurnResult.PlayedCard;
    var matching = Hand.Where(x => x.Color == currentDiscard.Color || x.Value == currentDiscard.Value || x.Color == CardColor.Wild).ToList();

    //We cannot play wild draw four unless there are no other matches.
    if(matching.All(x => x.Value == CardValue.DrawFour))
    {
        turn.Card = matching.First();
        turn.DeclaredColor = SelectDominantColor();
        turn.Result = TurnResult.WildCard;
        Hand.Remove(matching.First());

        return turn;
    }

    //Otherwise, we play the card that would cause the most damage to the next player.
    if(matching.Any(x=> x.Value == CardValue.DrawTwo))
    {
        turn.Card = matching.First(x => x.Value == CardValue.DrawTwo);
        turn.Result = TurnResult.DrawTwo;
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(turn.Card);

        return turn;
    }

    if(matching.Any(x => x.Value == CardValue.Skip))
    {
        turn.Card = matching.First(x => x.Value == CardValue.Skip);
        turn.Result = TurnResult.Skip;
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(turn.Card);

        return turn;
    }

    if (matching.Any(x => x.Value == CardValue.Reverse))
    {
        turn.Card = matching.First(x => x.Value == CardValue.Reverse);
        turn.Result = TurnResult.Reversed;
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(turn.Card);

        return turn;
    }

    // At this point the player has a choice of sorts
    // Assuming he has a match on color AND a match on value 
    // (with none of the matches being attacking cards), 
    // he can choose which to play.  For this modeling practice, we'll assume 
    // that playing the match with MORE possible matches from his hand 
    // is the better option.

    var matchOnColor = matching.Where(x => x.Color == currentDiscard.Color);
    var matchOnValue = matching.Where(x => x.Value == currentDiscard.Value);
    if(matchOnColor.Any() && matchOnValue.Any())
    {
        var correspondingColor = Hand.Where(x => x.Color == matchOnColor.First().Color);
        var correspondingValue = Hand.Where(x => x.Value == matchOnValue.First().Value);
        if(correspondingColor.Count() >= correspondingValue.Count())
        {
            turn.Card = matchOnColor.First();
            turn.DeclaredColor = turn.Card.Color;
            Hand.Remove(matchOnColor.First());

            return turn;
        }
        else //Match on value
        {
            turn.Card = matchOnValue.First();
            turn.DeclaredColor = turn.Card.Color;
            Hand.Remove(matchOnValue.First());

            return turn;
        }
    }
    else if(matchOnColor.Any()) //Play the match on color
    {
        turn.Card = matchOnColor.First();
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(matchOnColor.First());

        return turn;
    }
    else if(matchOnValue.Any()) //Play the match on value
    {
        turn.Card = matchOnValue.First();
        turn.DeclaredColor = turn.Card.Color;
        Hand.Remove(matchOnValue.First());

        return turn;
    }

    //Play regular wilds last.  If a wild becomes our last card, we win on the next turn!
    if (matching.Any(x => x.Value == CardValue.Wild))
    {
        turn.Card = matching.First(x => x.Value == CardValue.Wild);
        turn.DeclaredColor = SelectDominantColor();
        turn.Result = TurnResult.WildCard;
        Hand.Remove(turn.Card);

        return turn;
    }

    //This should never happen
    turn.Result = TurnResult.ForceDraw;
    return turn;
}

Selecting the Dominant Color

In both the Wild and non-Wild versions of this method, we see a call to SelectDominantColor(), which returns the color that appears most often in the current players' hand. Here's that method:

private CardColor SelectDominantColor()
{
    if (!Hand.Any())
    {
        return CardColor.Wild; //Null case, causes a passthrough in the calling method
    }
    var colors = Hand.GroupBy(x => x.Color).OrderByDescending(x => x.Count());
    return colors.First().First().Color;
}

Drawing a Card

We've now completed implementation Player Logic Steps 2, 3, and 4, so let's move on to Step 5:

Step 5: If the player has no cards to play, s/he draws a single card from the draw pile. If the drawn card can be played, s/he plays that card.

We now need to implement the DrawCard() method defined earlier. This method turns out to be surprisingly simple now that PlayMatchingCard() is already implemented. Here it is:

private PlayerTurn DrawCard(PlayerTurn previousTurn, CardDeck drawPile)
{
    PlayerTurn turn = new PlayerTurn();
    var drawnCard = drawPile.Draw(1);
    Hand.AddRange(drawnCard);

    if (HasMatch(previousTurn.Card))  //If the drawn card matches the discard, play it
    {
        turn = PlayMatchingCard(previousTurn.Card);
        turn.Result = TurnResult.ForceDrawPlay;
    }
    else
    {
        turn.Result = TurnResult.ForceDraw;
        turn.Card = previousTurn.Card;
    }

    return turn;
}

And with that, there's only one thing left to do: implement the decision tree!

Putting It All Together

Now that the individual player actions are all scripted, the only thing we have left to do is implement a method which will be called by the Game Manager (which we will implement fully in Part 3 of this series) and will make the Player decide what action to take. The method is called PlayTurn() and here it is:

public PlayerTurn PlayTurn(PlayerTurn previousTurn, CardDeck drawPile)
{
    PlayerTurn turn = new PlayerTurn();
    if (previousTurn.Result == TurnResult.Skip
        || previousTurn.Result == TurnResult.DrawTwo
        || previousTurn.Result == TurnResult.WildDrawFour)
    {
        return ProcessAttack(previousTurn.Card, drawPile);
    }
    else if ((previousTurn.Result == TurnResult.WildCard 
                || previousTurn.Result == TurnResult.Attacked 
                || previousTurn.Result == TurnResult.ForceDraw) 
                && previousTurn.Card.Color == CardColor.Wild
                && HasMatch(previousTurn.DeclaredColor))
    {
        turn = PlayMatchingCard(previousTurn.DeclaredColor);
    }
    else if (HasMatch(previousTurn.Card))
    {
        turn = PlayMatchingCard(previousTurn.Card);
    }
    else //Draw a card and see if it can play
    {
        turn = DrawCard(previousTurn, drawPile);
    }

    DisplayTurn(turn);
    return turn;
}

Summary

Well, would you look at that! We've now completed our Players' behavior (stupid jackasses that they are), and all that's left to do is wire the entire thing together and play some UNO! In the final part of this series, we'll do just that.

Don't forget to check out the GitHub repository for this series.

Happy Coding!