Welcome to another edition of my long-running Modeling Practice series!
In this series, I take common board and card games and attempt to model them using C# and .NET. We have previously modeled Candy Land, Minesweeper, UNO, Battleship, the card game War, and Connect Four in Blazor.
In this edition of the series, we take on the biggest, most complex board game I've ever tried to model: Ticket to Ride.

You can also buy it on Amazon, if you wish (affiliate link):
Ticket To Ride - Play With AlexaI may have bitten off more than I can chew with this one, but there's only one way to find out! Let's go!
The Sample Project
As always with my Modeling Practice series, there is a sample project over on GitHub that shows the code we will use in this and future blog posts in this series. Check it out!
Series Outline
The post you are reading is Part 1 of a six-part series on modeling the board game Ticket to Ride. In future posts, we will cover:
- Part 2: Classes and Board Setup
- Part 3: Finding Ideal Routes
- Part 4: Player Claiming Routes
- Part 5: Player Drawing Cards
- Part 6: Structure, Scoring, and Drawbacks
A Quick Reminder
Remember that the goal of these posts is not to produce a perfectly-working simulation of Ticket to Ride. I honestly doubt that is even within the range of my meagar capabilities, and you will see at the end of the series that the resulting simulation is far from perfect.
Rather, the goal of this series and all Modeling Practice posts is to practice taking a real-world bounded problem (such as a board game) and translating it into C# classes, objects, and code.
With that out of the way, let's discuss how we play a game of Ticket to Ride!
Rules of the Game
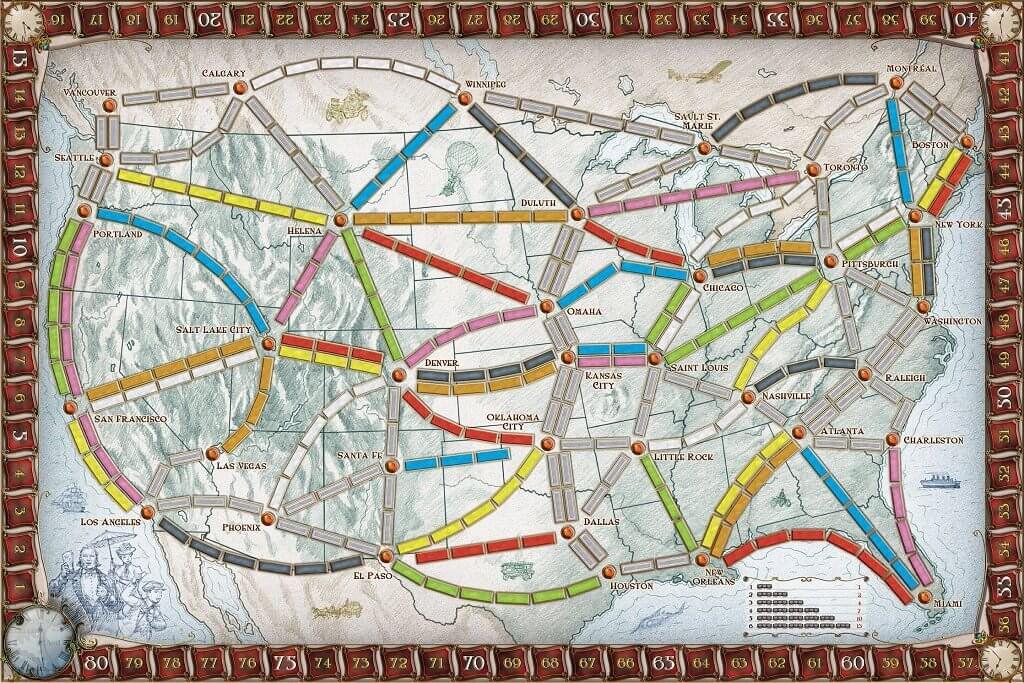
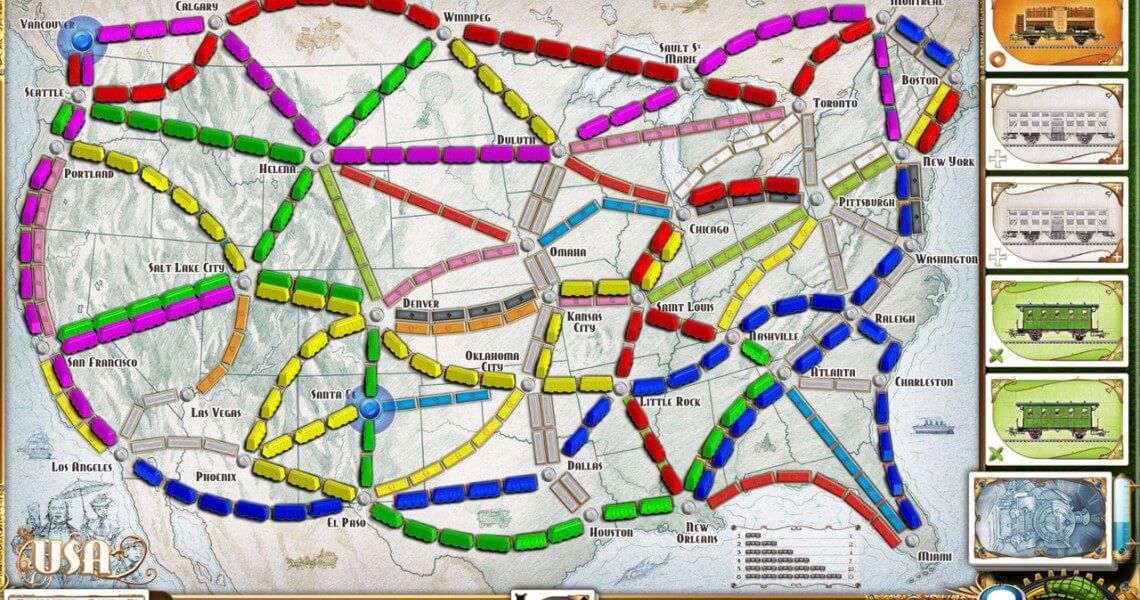
The basic goal of Ticket to Ride is to connect cities to each other by "claiming" train routes. The game board looks like this:
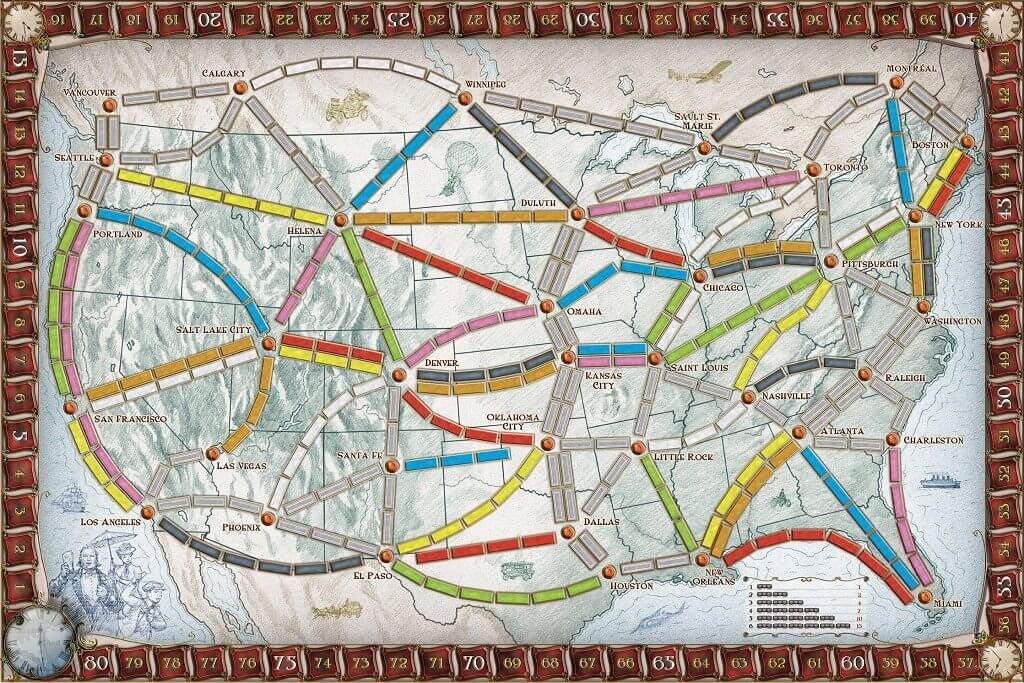
Various North American cities are labeled and connected by "routes". Routes are then colored one of nine colors: red, blue, orange, yellow, green, purple, black, white, and grey.
Players claim routes by using "train cards", and said cards can have one of eight different colors.

There is also a "locomotive" card, which acts as a wild and can be used in place of any color.

Let's say you wanted to claim the route St. Louis to Pittsburgh (middle-right of the board), as shown here:
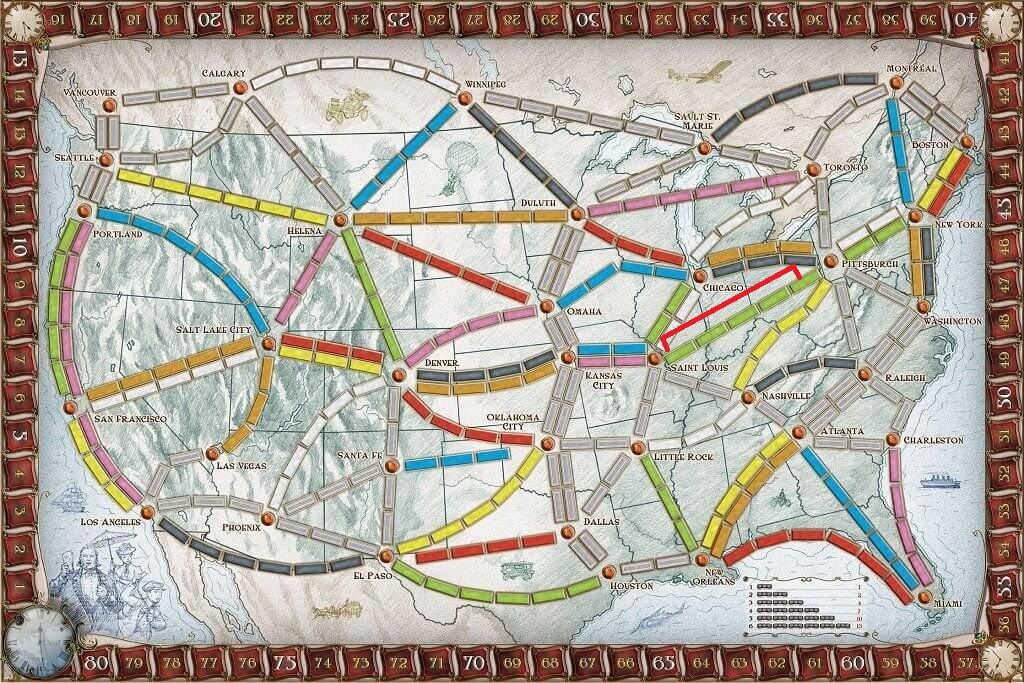
That route requires five green cards, so you could use five green train cards, or four green cards and one locomotive card, or some combination thereof.
Grey Routes
There are also "grey" routes, or routes which do not have one of the main eight colors. These routes can be claimed by using any one color, provided you have enough cards of that color.
For example, say you wanted to claim the route Winnipeg to Sault Ste. Marie (top-center of the board), as shown here:
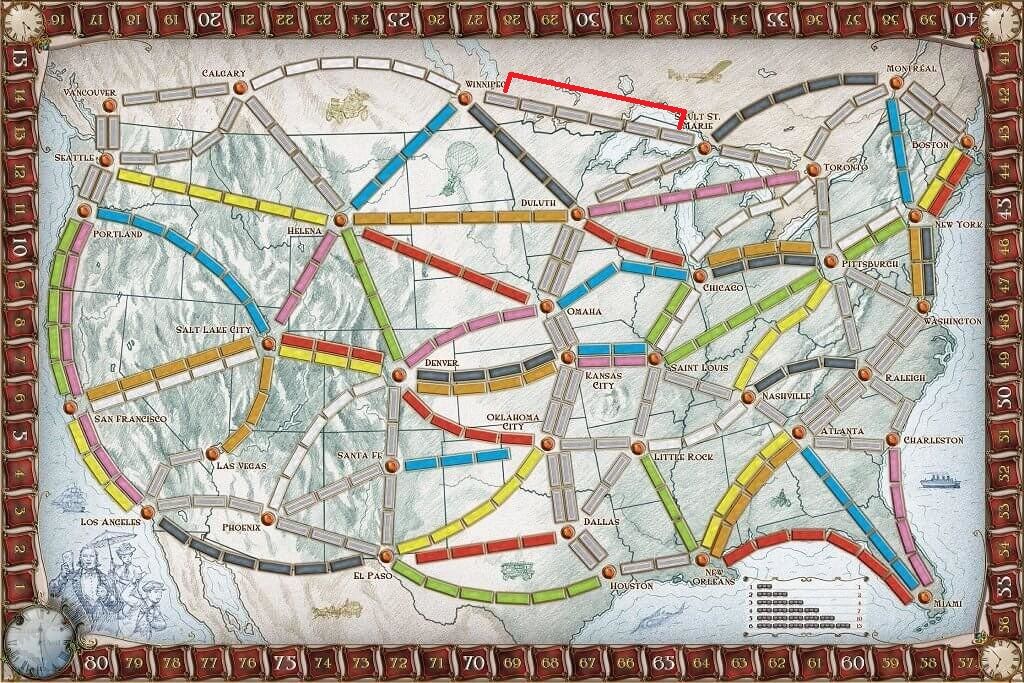
That route has six grey spaces, so we could use six black, or six yellow, or four orange and two locomotives, or any combination of color cards and locomotives that add up to six.
Double Routes
Some of the cities are connected by "double" routes. If you look at the "Midwest spine" of cities between Duluth and Houston in the middle of the board, almost all of them are directly connected by double routes. Along the west coast, cities between Los Angeles and Vancouver are also connected by double routes. Many more examples can be found on the game board.
In a game with 4 or 5 players, the double routes cannot both be claimed by the same player. For example, Player 1 could not claim both the black and orange routes between Chicago and Pittsburgh. Our sample project will use 4 players, so we will need to ensure that one player cannot claim both routes in a double-route set.
Board Route Points
Each board route is worth a certain number of points:
- One-car routes are worth 1 point.
- Two-car routes are worth 2 points.
- Three-car routes are worth 4 points.
- Four-car routes are worth 7 points.
- Five-car routes are worth 10 points.
- Six-car routes are worth 15 points.
Destination Cards
At the beginning of the game, each player is dealt three "destination cards". These cards are goals which the player will try to fulfill by connecting two distant cities.

Each card also has a point value, which is added to the player's score if they have connected the two cities ("finished" the card) by the end of the game. Destination cards which have not been finished have their values subtracted from the player's score.
Example Scoring
Let's say we are the red player, and at the end of the game we have the following destination cards:
Duluth to Houston, 8 Points
Chicago to New Orleans, 7 Points
Dallas to New York, 11 Points
Denver to Pittsburgh, 11 Points
And we have claimed the following routes:
Duluth to Omaha, 2 Points
Omaha to Kansas City, 2 Points
Kansas City to Oklahoma City, 2 Points
Oklahoma City to Dallas, 2 Points
Dallas to Houston, 1 Point
Houston to New Orleans, 2 Points
Omaha to Chicago, 7 Points
Chicago to Pittsburgh, 4 Points
Pittsburgh to Washington, 2 Points
New York to Washington, 2 Points
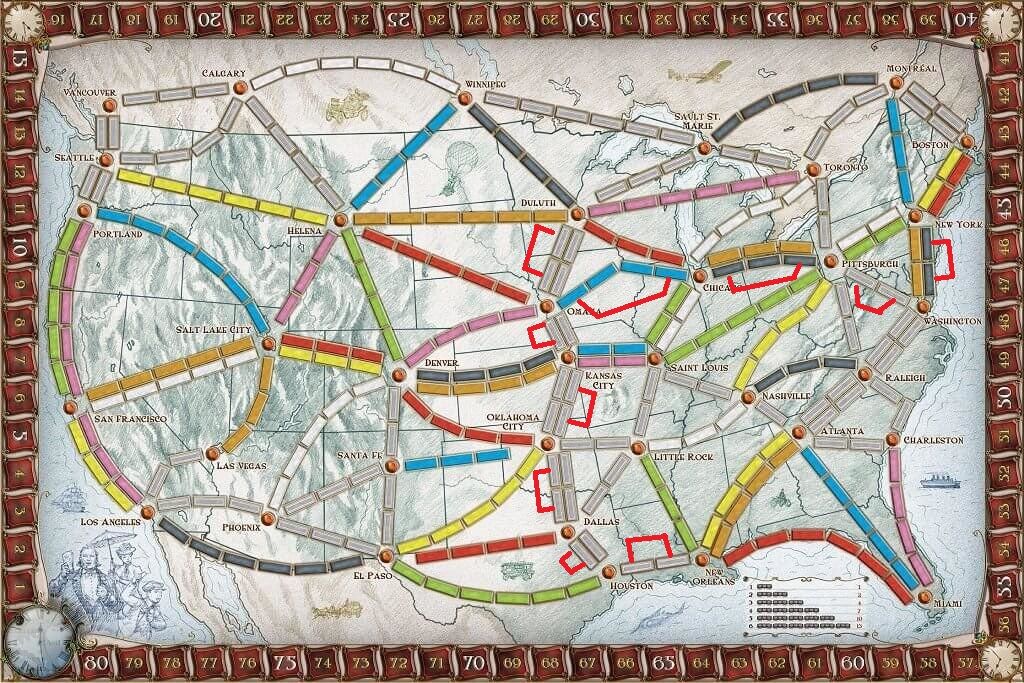
In this example, we have "finished" all our destination cards except one, Denver to Pittsburgh, so our final score would be 26 (for the routes) + 26 (for the completed destination cards) - 11 (for the incomplete destination card) = 41.
Player Turns
On their turn, players may do one of three things:
- They may "claim" a route, which means discarding the appropriate number of colored train cards and/or locomotives to place their trains on a given route.
- They may draw three (3) new destination cards. When they do this, they may examine the cards and return up to two of them to the destination card draw pile.
- They may draw new train cards.
Drawing New Train Cards
Drawing new train cards is a whole process unto itself.
"Shown" Cards
During the game, at any time there are five cards that are face-up on the table. These cards are the "shown" cards, and players may choose to take up to two of them on their turn.

If one of the shown cards is a locomotive (or "wild" card), the player may take it, but then s/he cannot take any other cards.
If the player chooses, they may take only one of the shown cards and one from the draw pile, or take two cards from the draw pile. At most, a player will get two train cards on their turn, if they choose to draw.
Summary
In short:
- Cities are connected by routes, which have colors.
- Train cards are used to "claim" routes, which add points to the player's score.
- Destination cards are "goals" which, if not completed, subtract from the player's score.
- On their turn, players may either draw new destination cards, claim a route, or draw train cards.
- Players may not claim both parts of a "double" route.
- Each player starts with 48 train cars. The game enters the "final turn" when a single player has 2 or less train cars remaining.
In the next part of this series, we're going to start reading into these rules and objects in order to create C# classes which represent them. We will also see how to set up a game that can be played, with destination cards, train cards, and board routes. Finally, we'll begin to think about the various ways our players can make decisions as to which routes they want, which train card colors they desire, and what to do when it is their turn.
Don't forget to check out the sample project over on GitHub!
If this post helped you (or if you just like seeing board games made into programming projects), would you consider buying me a coffee? Your support funds all of my projects and helps me keep traditional ads off this site. Thanks!

Happy Coding!