I've been coding with C# and ASP.NET for a long time. In all of that time, I haven't really had a need to figure out the nitty-gritty differences between float and double, or between decimal and pretty much any other type. I've just used them as I see fit, and hope that's how they were meant to be used.
Until recently, anyway. Recently, as I was attending the AngleBrackets conference, and one of the coolest parts of attending that conference is getting to be in an in-depth workshop. My particular workshop was called I Will Make You A Better C# Programmer by Kathleen Dollard, and let me tell you, she emphatically did.
One of the most interesting things I learned at Kathleen's session was that the .NET number types don't always behave the way I think they do. In this post, I'm going to walk through a few (a VERY few) of Kathleen's examples and try to explain why .NET has so many different number types and what they are each for. Come along as I (with her code) attempt to show what the number types are, and what they are used for!
The Sample Project
As with most of my code-focused posts, there is a sample project for this post over on GitHub. Check it out!
The Number Types in .NET
Let's start with a review of the more common number types in .NET. Here's a few of the basic types:
- Int16 (aka short): A signed integer with 16 bits (2 bytes) of space available.
- Int32 (aka int): A signed integer with 32 bits (4 bytes) of space available.
- Int64 (aka long): A signed integer with 64 bits (8 bytes) of space available.
- Single (aka float): A 32-bit floating point number.
- Double (aka double): A 64-bit floating-point number.
- Decimal (aka decimal): A 128-bit floating-point number with a higher precision and a smaller range than Single or Double.
There's an interesting thing to point out when comparing double and decimal: the range of double is ±5.0 × 10−324 to ±1.7 × 10308, while the range of decimal is (-7.9 x 1028 to 7.9 x 1028) / (100 to 28). In other words, the range of double is several times larger than the range of decimal. The reason for this is that they are used for quite different things.
Precision vs Accuracy
One of the concepts that's really important to discuss when dealing with .NET number types is that of precision vs. accuracy. To make matters more complicated, there are actually two different definitions of precision, one of which I will call arithmetic precision.
- Precision refers to the closeness of two or more measurements to each other. If you measure something five times and get exactly 4.321 each time, your measurement can be said to be very precise.
- Accuracy refers to the closeness of a value to standard or known value. If you measure something, and find it's weight to be 4.7kg, but the known value for that object is 10kg, your measurement is not very accurate.
- Arithmetic precision refers to the number of digits used to represent a number (e.g. how many numbers after the decimal are used). The number 9.87 is less arithmetically precise than the number 9.87654332.
We always need mathematical operations in a computer system to be accurate; we cannot ever expect 4 x 6 = 32. Further, we also need these calculations to be precise using the common term; 4 x 6 must always be precisely 24 no matter how many times we make that calculation. However, the extent to which we want our systems to be either arithmetically precise has a direct impact on the performance of those system.
If we lose some arithmetic precision, we gain performance. The reverse is also true: if we need values to be arithmetically precise, we will spend more time calculating those values. Failing to take this into account can lead to incredible performance problems, problems which can be solved by using the correct type for the correct problem. These kinds of issues are most clearly shown during Test 3 later in this post.
Why Is int The Default?
In the following line of code, number will always be of type int:
var number = 5;
But why is that? Why not a short, since that takes up less space? Or maybe a long, since that will represent nearly any integer we could possibly use?
Turns out the answer is, as it often is, performance. .NET optimizes your code to run in a 32-bit architecture, which means that any operations involving 32-bit integers will by definition be more performant than either 16-bit or 64-bit operations. I expect that this will change as we move toward a 64-bit architecture being standard, but for now, 32-bit integers are the most performant option.
Number Type Differences
One of the ways we can start to see the inherent differences between the above types is by trying to use them in calculations. We're going to see three different tests, each of which will reveal a little more about how .NET uses each of these types.
Test 1: Division
Let's start with a basic example using division. Consider the following code:
private void DivisionTest1()
{
int maxDiscountPercent = 30;
int markupPercent = 20;
Single niceFactor = 30;
double discount = maxDiscountPercent * (markupPercent / niceFactor);
Console.WriteLine("Discount (double): ${0:R}", discount);
}
private void DivisionTest2()
{
byte maxDiscountPercent = 30;
int markupPercent = 20;
int niceFactor = 30;
int discount = maxDiscountPercent * (markupPercent / niceFactor);
Console.WriteLine("Discount (int): ${0}", discount);
}
Note that the only thing that's really different about these two methods are the types of the local variables.
Now here's the question: what will the discount be in each of these methods?
If you said that they'll both be $20, you're missing something very important.
The problem line is this one, from DivisionTest2():
int discount = maxDiscountPercent * (markupPercent / niceFactor);
Here's the problem: because markupPercent is declared as an int (which in turn makes it an Int32), when you divide an int by another int, the result will be an int, even when we would logically expect it to be something like a double. .NET does this by truncating the result, so because 20 / 30 = 0.6666667, what you get back is 0 (and anything times 0 is 0).
In short, the discount for DivisionTest1 is the expected $20, but the discount for DivisionTest2 is $0, and the only difference between them is what types are used. That's quite a difference, yes?
Test 2 - Double Addition
Now we get to see something weird, and it involves the concept of arithmetic precision from earlier. Here's the next method:
public void DoubleAddition()
{
Double x = .1;
Double result = 10 * x;
Double result2 = x + x + x + x + x + x + x + x + x + x;
Console.WriteLine("{0} - {1}", result, result2);
Console.WriteLine("{0:R} - {1:R}", result, result2);
}
Just by reading this code, we expect result and result2 to be the same: multiplying .1 x 10 should equal .1 + .1 + .1 + .1 + .1 + .1 + .1 + .1 + .1 + .1.
But there's another trick here, and that's the usage of the "{O:R}" string formatter. That's called the round-trip formatter, and it tells .NET to display all parts of this number to its maximum arithmetic precision.
If we run this method, what does the output look like?

By using the round-trip formatter, we see that the multiplication result ended up being exactly 1, but the addition result was off from 1 by a miniscule (but still potentially significant) amount. Question is: why does it do this?
In most systems, a number like 0.1 cannot be accurately represented using binary. There will be some form of arithmetic precision error when using a number such as this. Generally, said arithmetic precision error is not noticeable when doing mathematical operations, but the more operations you perform, the more noticeable the error is. The reason we see the error above is because for the multiplication portion, we only performed one operation, but for the addition portion, we performed ten, and thus caused the arithmetic precision error to compound each time.
Test 3 - Decimal vs Double Performance
Now we get to see something really interesting. I'm often approached by new .NET programmers with a question like the following: why should we use decimal over double and vice-versa? This test pretty clearly spells out when and why you should use these two types.
Here's the sample code:
private int iterations = 100000000;
private void DoubleTest()
{
Stopwatch watch = new Stopwatch();
watch.Start();
Double z = 0;
for (int i = 0; i < iterations; i++)
{
Double x = i;
Double y = x * i;
z += y;
}
watch.Stop();
Console.WriteLine("Double: " + watch.ElapsedTicks);
Console.WriteLine(z);
}
private void DecimalTest()
{
Stopwatch watch = new Stopwatch();
watch.Start();
Decimal z = 0;
for (int i = 0; i < iterations; i++)
{
Decimal x = i;
Decimal y = x * i;
z += y;
}
watch.Stop();
Console.WriteLine("Decimal: " + watch.ElapsedTicks);
Console.WriteLine(z);
}
For each of these types, we are doing a series of operations (100 million of them) and seeing how many ticks it takes for the double operation to execute vs how many ticks it takes for the decimal operations to execute. The answer is startling:
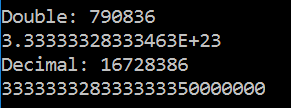
The operations involving double take 790836 ticks, while the operations involving decimal take a whopping 16728386 ticks. In other words, the decimal operations take 21 times longer to execute than the double operations. (If you run the sample project, you'll notice that the decimal operations take noticeably longer than the double ones).
But why? Why does double take so much less time in calculations than decimal does?
For one thing, double uses base-2 math, while decimal uses base-10 math. Base-2 math is much quicker for computers to calculate.
Further, double is concerned with is performance, while decimal is concerned with is precision. When using double, you are accepting a known trade-off: you won't be super precise in your calculations, but you will get an acceptable answer quickly. Whereas with decimal, precision is built into its type: it's meant to be used for money calculations, and guess how many people would riot if those weren't accurate down to the 23rd place after the decimal point.
In short, double and decimal are two totally separate types for a reason: one is for speed, and the other is for precision. Make sure you use the appropriate one at the appropriate time.
Summary
As can be expected from such a long-lived framework, .NET has several number types to help you with your calculations, ranging from simple integers to complex currency-based values. As always, it's important to use the correct tool for the job:
- Use
doublefor non-integer math where the most precise answer isn't necessary. - Use
decimalfor non-integer math where precision is needed (e.g. money and currency). - Use
intby default for any integer-based operations that can use that type, as it will be more performant thanshortorlong.
Don't forget to check out the sample project over on GitHub!
Also, if this post helped you, please consider buying me a coffee. Your support funds all of my projects and helps me keep traditional ads off this site. Thanks for your support!
Happy Coding!
Huge thanks to Kathleen Dollard (@kathleendollard) for providing the code samples and her invaluable insight into how to effectively explain what's going on in these samples. Check out her Pluralsight course for more!









