With our rules known and our setup complete, we now need to tackle a difficult problem in solving this game: how do we determine the ideal route between two cities?
The Sample Project
As always, there is a sample project on GitHub that has the code we will use here. Check it out!
Finding Ideal Routes
Let's imagine that we want to find the best route between San Francisco and Nashville. Both these locations are marked as 1 on the map below.
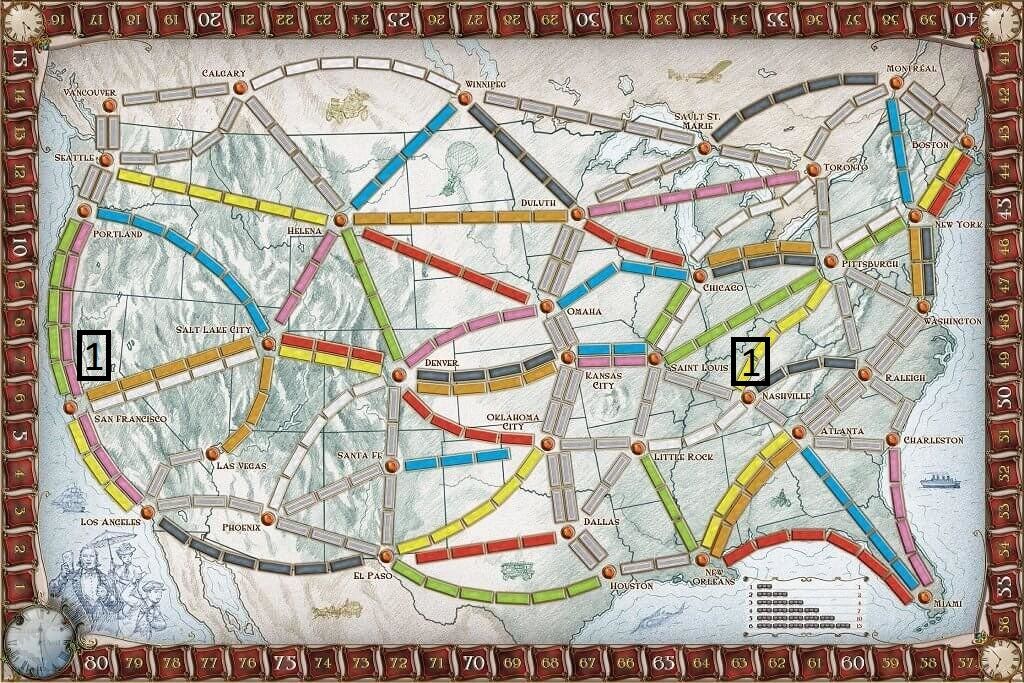
To start with, let's determine all the destinations we can reach from each of these cities. From San Francisco, we can reach Portland, Salt Lake City, and Los Angeles. From Nashville, we can reach St. Louis, Pittsburgh, Raleigh, Atlanta, and Little Rock. The "second-order" destinations look like this:
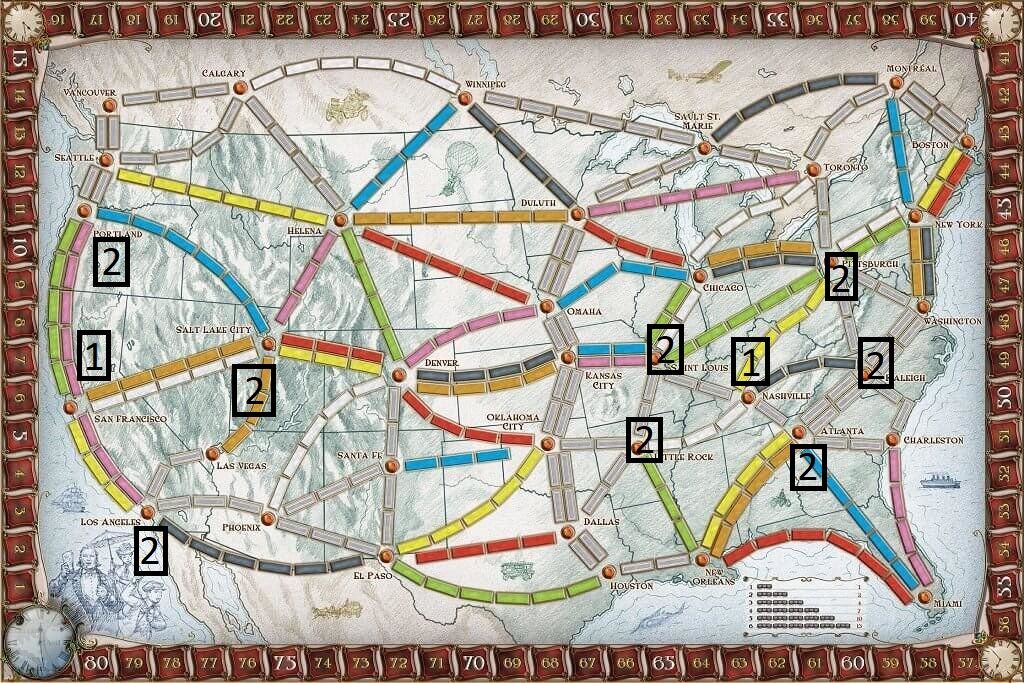
The idea is to continue doing this (i.e. looking at all destinations of all connected cities) until one or more cities show up on both sides.
Continuing this, the "third-order" destinations (i.e. every city connected to each of the second-order cities) would look like this:
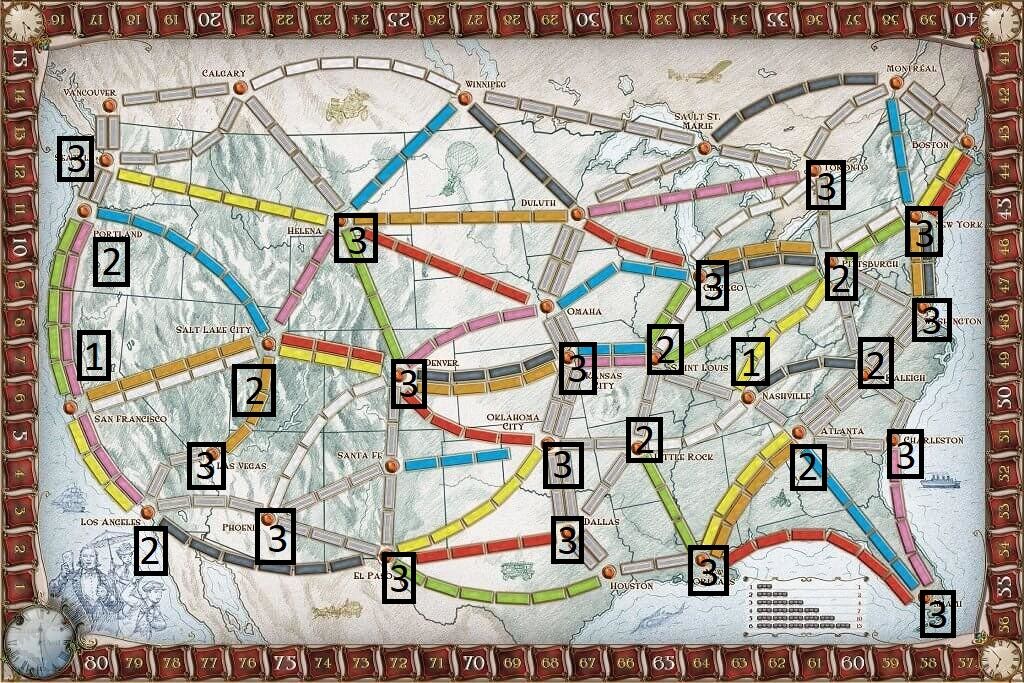
Now you might be thinking, "great! On the next order, we will have overlapping cities, and as such can find the connecting routes!" And you'd be right. From the overlapping cities we can isolate routes between San Francisco and Nashville.
Here are all the routes this "naive" algorithm would find:
San Francisco -> Salt Lake City -> Denver -> Kansas City -> Saint Louis -> Nashville (16 spaces)
San Francisco -> Salt Lake City -> Denver -> Oklahoma City -> Little Rock -> Nashville (17 spaces) (thank you to Joost Menger for finding this!)
San Francisco -> Los Angeles -> El Paso -> Dallas -> Little Rock -> Nashville (18 spaces)
San Francisco -> Los Angeles -> El Paso -> Oklahoma City -> Little Rock -> Nashville (19 spaces)
However, we know that these routes are not created equal. The first of these will be easiest to claim because the total length of that route is the smallest of the potential routes. Therefore, the "ideal" route will go through Denver, Kansas City, and Saint Louis.
This kind of algorithm will work perfectly fine if no one has claimed any routes yet. But what if some routes are already claimed?
Finding Best-Possible Routes
Let's imagine that the game is already well underway, and some routes have already been claimed.
We're going to try to connect Calgary (top-left of the board, near the number 20) to Denver (middle-left of the board). Note that several routes, including the most direct one, are already claimed by other players (specifically Calgary -> Helena, Helena -> Denver, Helena -> Omaha, and both Duluth -> Omaha routes)
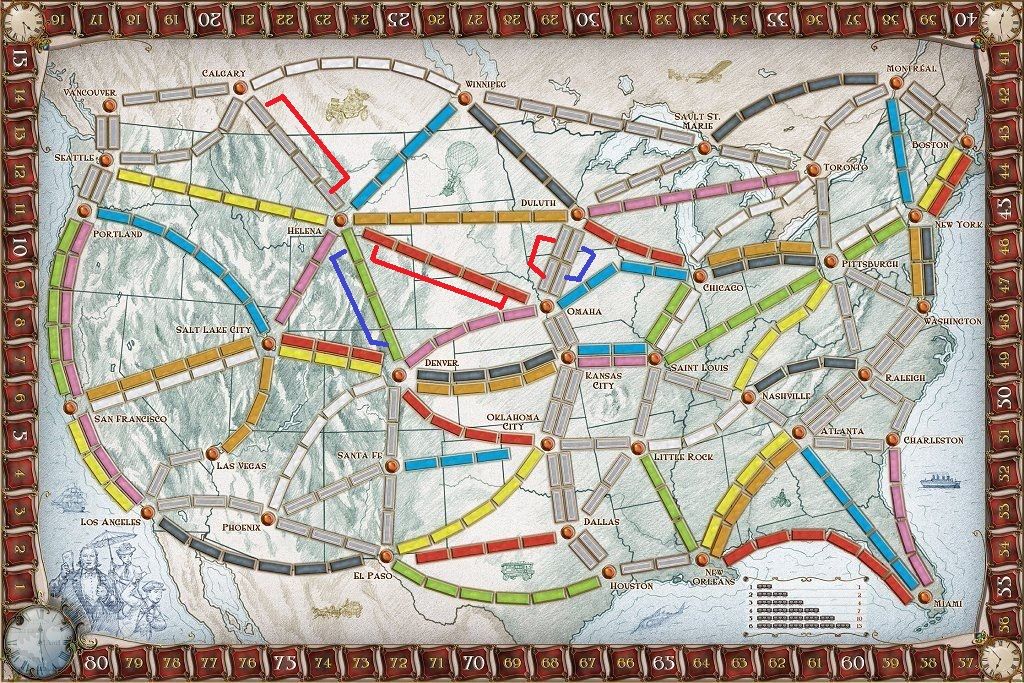
We would prefer to take the routes Calgary -> Helena -> Denver, because that takes the least number of cards and the least number of turns. But that's impossible now, because those routes are both claimed.
So if our first-order cities are Calgary and Denver, here's our second order cities, ignoring routes that are already claimed.
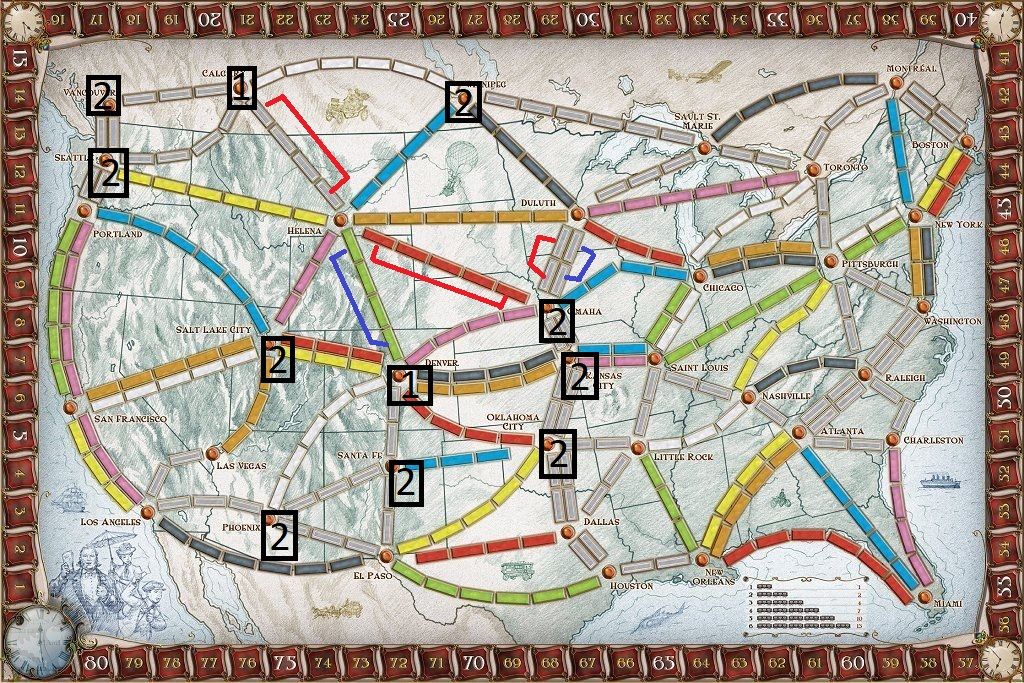
From Calgary, our second-order cities are Vancouver, Seattle, and Winnipeg. From Denver, our second-order cities are Salt Lake City, Omaha, Kansas City, Oklahoma City, Santa Fe, and Phoenix.
If we continue this, the algorithm will find the following paths:
Calgary -> Seattle -> Portland -> Salt Lake City -> Denver (14 spaces)
Calgary -> Seattle -> Helena -> Salt Lake City -> Denver (16 spaces)
Calgary -> Winnipeg -> Helena -> Salt Lake City -> Denver (16 spaces)
All these routes will take the same number of turns (4) to claim, However, we know that the first option is the best, because it takes the least amount of trains to claim those routes.
Here's the secret: the algorithm for both ideal routes and best possible routes is actually the same algorithm! The only difference is that for best-possible routes, the routes which have already been claimed are not even considered. It is like they do not exist in that case.
In short, we expand ever outward from both the origin and destination cities, until the list of cities we can reach from both sides (origin and destination) contains the same city. If there are many of these, we take the one with the least number of total spaces.
With all this in mind, let's start making this algorithm! Be warned, though: this implementation contains healthy doses of recursion.
The Code
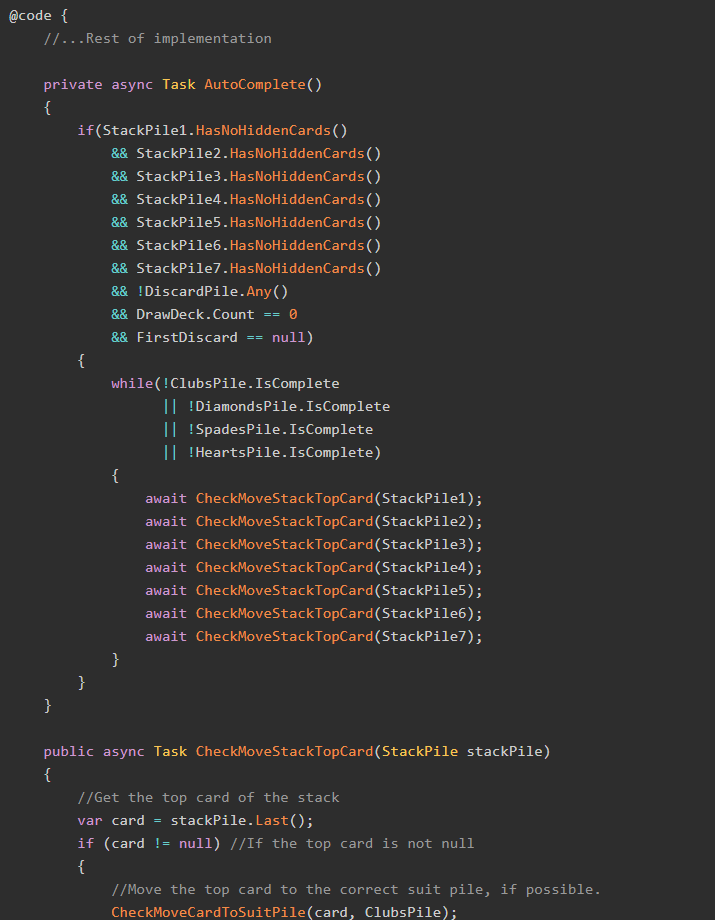
Remember the BoardRouteCollection class? I did say it would come in handy, and that starts now. Let's add a method FindIdealUnclaimedRoute to that class:
public class BoardRouteCollection
{
public List<BoardRoute> FindIdealUnclaimedRoute(City origin, City destination) { ... }
}This method will return the list of BoardRoute objects that comprise the "ideal" or shortest route between the two passed-in Cities.
In order to find the ideal route, we need to get the collection of cities that a given city can connect to. That requires a new method:
public class BoardRouteCollection
{
public List<BoardRoute> FindIdealUnclaimedRoute(City origin, City destination) { /*...Not implemented yet*/ }
public List<CityLength> GetConnectingCities(City origin)
{ ... }
}There's a new class now: CityLength. When I wrote this method, I had no way to keep track of how many spaces we would need to claim in order to move from one city to another. So I created this class to do that for me.
public class CityLength
{
public City City { get; set; }
public int Length { get; set; }
}Origin or Destination?
For the given origin and destination, let's get all the connecting cities by querying the Board Routes:
public class BoardRouteCollection
{
public List<BoardRoute> Routes { get; set; } = new List<BoardRoute>();
public List<CityLength> GetConnectingCities(City startingCity)
{
var destinations = Routes.Where(x => x.Origin == startingCity
&& !x.IsOccupied)
.OrderBy(x => x.Length)
.Select(x => new CityLength()
{
City = x.Destination,
Length = x.Length
})
.ToList();
var origins = Routes.Where(x => x.Destination == startingCity
&& !x.IsOccupied)
.OrderBy(x => x.Length)
.Select(x => new CityLength()
{
City = x.Origin,
Length = x.Length
})
.ToList();
destinations.AddRange(origins);
return destinations.Distinct().OrderBy(x => x.Length).ToList();
}
}No Possible Routes
Here's the first problem: it is entirely possible that no routes connect the two cities. For example, what if all three routes into Miami are claimed already, and we have the destination card Los Angeles to Miami? Well then we are out of luck, and the algorithm won't return any routes.
It is also possible that the passed-in origin and destination are the same city. In that situation, we will return an empty set of routes (this is due to the recursion coming up later in the method).
First Part of FindIdealUnclaimedRoute
Here's the first part of the FindIdealUnclaimedRoute() method:
public List<BoardRoute> FindIdealUnclaimedRoute(City origin, City destination)
{
List<BoardRoute> returnRoutes = new List<BoardRoute>();
if (origin == destination)
{
return returnRoutes;
}
//Get the initial lists of connecting cities
//from the origin and destination.
var masterOriginList = GetConnectingCities(origin);
var masterDestinationList = GetConnectingCities(destination);
//If these methods return no routes,
//there are no possible routes to finish.
//So, we return an empty list.
if(!masterOriginList.Any() || !masterDestinationList.Any())
{
return new List<BoardRoute>();
}
//...More to come
}But now the implementation gets more complicated.
Getting Direct Routes
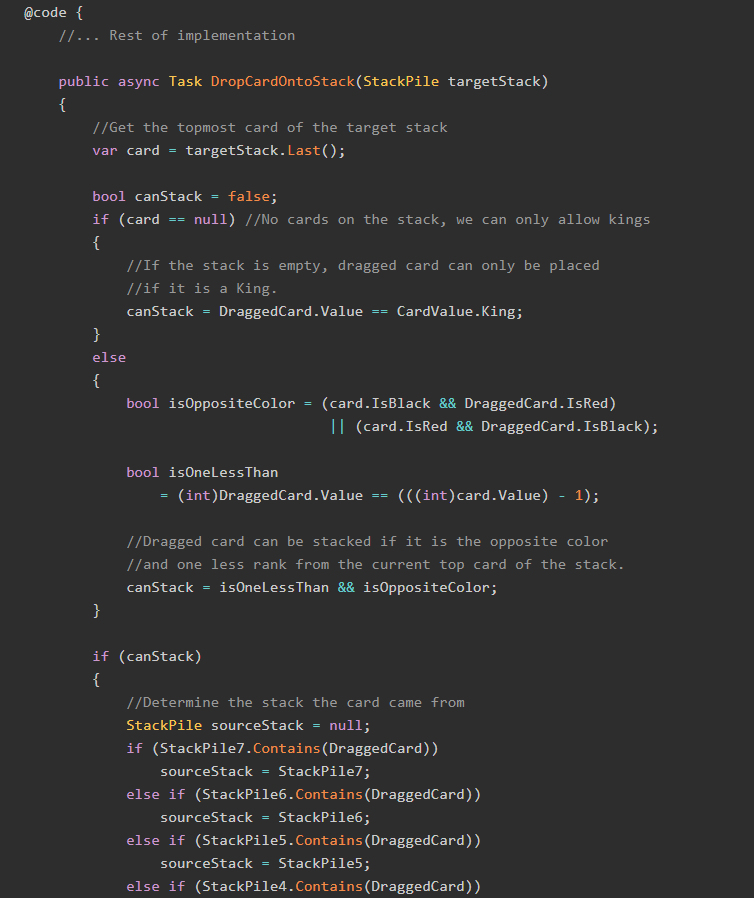
We need a small utility method now. In order to see if any of the cities between the origin list and destination list connect, we can check if there are any available "direct" routes between them. Such a method looks like this:
public BoardRoute GetDirectRoute(City origin, City destination)
{
var route = Routes.Where(x =>
(x.Origin == origin && x.Destination == destination && !x.IsOccupied)
|| (x.Origin == destination && x.Destination == origin && !x.IsOccupied))
.FirstOrDefault();
return route;
}Stepping Through the Orders
Now that we have the possible destinations from both the original origin and original destination, we should "step through the orders" to find a city that can be reached from both sides.
public List<BoardRoute> FindIdealUnclaimedRoute(City origin, City destination)
{
List<BoardRoute> returnRoutes = new List<BoardRoute>();
if (origin == destination)
{
return returnRoutes;
}
//Get the initial lists of connecting cities
//from the origin and destination
var masterOriginList = GetConnectingCities(origin);
var masterDestinationList = GetConnectingCities(destination);
//If these methods return no routes,
//there are no possible routes to finish.
//So, we return an empty list
if(!masterOriginList.Any() || !masterDestinationList.Any())
{
return new List<BoardRoute>();
}
//Get the cities
var originCitiesList = masterOriginList.Select(x => x.City);
var destCitiesList = masterDestinationList.Select(x => x.City);
bool targetOrigin = true;
//We want to break the loop when a city appears in both the
//origin city list and the destination city list, because
//that means this city is reachable from both.
//There is a possibility that this algorithm will fall into a loop,
//traversing continuously over the same routes
//without finding a connecting route.
//The check against originCitiesList.Count() is to fix that situation.
while (!originCitiesList.Intersect(destCitiesList).Any()
&& originCitiesList.Count() < 500)
{
if (targetOrigin == true)
{
var copyMaster = new List<City>(originCitiesList);
foreach (var originCity in copyMaster)
{
masterOriginList.AddRange(GetConnectingCities(originCity));
}
}
else
{
var copyMaster = new List<City>(destCitiesList);
foreach (var destCity in copyMaster)
{
masterDestinationList.AddRange(GetConnectingCities(destCity));
}
}
targetOrigin = !targetOrigin;
}
//It is possible that there are no connecting routes left.
//In that case, the collections for master cities get very large
//If they get very large, assume no connections exist.
if (originCitiesList.Count() >= 500)
{
return new List<BoardRoute>();
}
//This is the city reachable from both the origin and destination
var midpointCity = originCitiesList.Intersect(destCitiesList).First();
}Since this algorithm can now reliably detect the so-called "midpoint" city, we can call it recursively to find the routes between any two points on the map.
The Final Code
Here's the final, complete code for the FindIdealUnclaimedRoute() method:
public List<CityLength> GetConnectingCities(City startingCity)
{
var destinations = Routes.Where(x => x.Origin == startingCity
&& !x.IsOccupied)
.OrderBy(x => x.Length)
.Select(x => new CityLength()
{
City = x.Destination,
Length = x.Length
})
.ToList();
var origins = Routes.Where(x => x.Destination == startingCity
&& !x.IsOccupied)
.OrderBy(x => x.Length)
.Select(x => new CityLength()
{
City = x.Origin, \
Length = x.Length
})
.ToList();
destinations.AddRange(origins);
return destinations.Distinct().OrderBy(x => x.Length).ToList();
}
public List<BoardRoute> FindIdealUnclaimedRoute(City origin, City destination)
{
List<BoardRoute> returnRoutes = new List<BoardRoute>();
if (origin == destination)
{
return returnRoutes;
}
//Get the initial lists of connecting cities
// from the origin and destination
var masterOriginList = GetConnectingCities(origin);
var masterDestinationList = GetConnectingCities(destination);
//If these methods return no routes,
// there are no possible routes to finish.
//So, we return an empty list
if(!masterOriginList.Any() || !masterDestinationList.Any())
{
return new List<BoardRoute>();
}
//Get the cities
var originCitiesList = masterOriginList.Select(x => x.City);
var destCitiesList = masterDestinationList.Select(x => x.City);
bool targetOrigin = true;
//There is a possibility that this algorithm will fall into a loop,
//traversing continuously over the same routes
//without finding a connecting route
//The check against originCitiesList.Count() is to fix that situation.
while (!originCitiesList.Intersect(destCitiesList).Any()
&& originCitiesList.Count() < 500)
{
if (targetOrigin == true)
{
var copyMaster = new List<City>(originCitiesList);
foreach (var originCity in copyMaster)
{
masterOriginList.AddRange(GetConnectingCities(originCity));
}
}
else
{
var copyMaster = new List<City>(destCitiesList);
foreach (var destCity in copyMaster)
{
masterDestinationList.AddRange(GetConnectingCities(destCity));
}
}
targetOrigin = !targetOrigin;
}
//It is possible that there are no connecting routes left.
//In that case, the collections for master cities get very large
//If they get very large, assume no connections exist.
if (originCitiesList.Count() >= 500)
{
return new List<BoardRoute>();
}
var midpointCity = originCitiesList.Intersect(destCitiesList).First();
var originDirectRoute = GetDirectRoute(origin, midpointCity);
var destinationDirectRoute = GetDirectRoute(midpointCity, destination);
//If a direct route exists, add it to the collection being returned
if (originDirectRoute != null)
{
returnRoutes.Add(originDirectRoute);
}
if(destinationDirectRoute != null)
{
returnRoutes.Add(destinationDirectRoute);
}
//If no direct route exists, recursively call this method
//until such a route is found or we determine that no such routes exist.
if (originDirectRoute == null)
{
returnRoutes.AddRange(FindIdealUnclaimedRoute(origin, midpointCity));
}
if (destinationDirectRoute == null)
{
returnRoutes.AddRange
(FindIdealUnclaimedRoute(midpointCity, destination));
}
return returnRoutes;
}
public BoardRoute GetDirectRoute(City origin, City destination)
{
var route = Routes.Where(x =>
(x.Origin == origin && x.Destination == destination && !x.IsOccupied)
|| (x.Origin == destination && x.Destination == origin && !x.IsOccupied))
.FirstOrDefault();
return route;
}Summary
In this third part of our Ticket to Ride C# Modeling Practice series, we implemented a "find the ideal route" algorithm that can find an ideal route between any two cities on the Ticket to Ride game board, even if some routes between them are already claimed.
In the next part of this series, the real work starts. We will use our ideal-route-finding algorithm to help implement player behavior, including how they determine which routes they want to claim and which colors they choose to draw.

Don't forget to check out the sample project over on GitHub!
Happy Coding!